Câu hỏi:
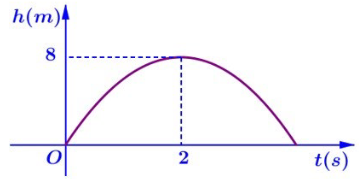
10/03/2025 813Khi một quả bóng được đá lên, nó sẽ đạt đến độ cao nào đó rồi rơi xuống. Hình sau minh họa quỹ đạo của quả bóng là một phần của cung parabol trong mặt phẳng tọa độ Oth, trong đó t là thời gian (tính bằng giây) kể từ khi quả bóng được đá lên và h là độ cao (tính bằng mét) của quả bóng. Giả thiết rằng quả bóng được đá từ mặt đất. Biết rằng tại thời điểm 2 giây, quả bóng đó lên đến vị trí cao nhất là 8 m rồi bắt đầu rơi xuống. Ở giây thứ bao nhiêu thì độ cao của quả bóng khi rơi xuống bằng 1,875 m.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
Trả lời: 3,75
Quỹ đạo của quả bóng là một phần parabol có dạng: \(h\left( t \right) = a{t^2} + bt\).
Khi \(t = 2\) quả bóng lên đến vị trí cao nhất là 8m.
Suy ra \(\left\{ \begin{array}{l} - \frac{b}{{2a}} = 2\\4a + 2b = 8\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}4a + b = 0\\4a + 2b = 8\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}a = - 2\\b = 8\end{array} \right.\). Do đó \(h\left( t \right) = - 2{t^2} + 8t\).
Khi \(h = 1,875\) thì \( - 2{t^2} + 8t = 1,875\)\( \Leftrightarrow t = 0,25\) hoặc \(t = 3,75\).
Vậy khi \(t = 3,75\) giây thì độ cao của quả bóng khi rơi xuống bằng 1,875 m.
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
- Trọng tâm Toán, Văn, Anh 10 cho cả 3 bộ KNTT, CTST, CD VietJack - Sách 2025 ( 13.600₫ )
- Trọng tâm Lí, Hóa, Sinh 10 cho cả 3 bộ KNTT, CTST và CD VietJack - Sách 2025 ( 40.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
a) Đ, b) Đ, c) S, d) Đ
a) Số phần tử của không gian mẫu bằng \(C_{12}^5\).
b) Để lấy được 5 viên bi cùng màu thì 5 viên bi lấy được có màu xanh.
Do đó số phần tử của biến cố “5 viên bi lấy ra cùng màu” là \(C_6^5\).
c) Xác suất của biến cố “5 viên bi lấy ra không có bi vàng” là \(P = \frac{{C_{10}^5}}{{C_{12}^5}} = \frac{7}{{22}}\).
d) Xác suất của biến cố “5 viên bi lấy ra có ít nhất một bi vàng” là \(P = 1 - \frac{7}{{22}} = \frac{{15}}{{22}}\).
Lời giải
Đáp án đúng là: A
Dựa vào đồ thị hàm số ta thấy hàm số đã cho nghịch biến trên khoảng \(\left( { - \infty ;1} \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
12 Bài tập Ứng dụng của hàm số bậc hai để giải bài toán thực tế (có lời giải)
-
10 Bài tập Ứng dụng ba đường conic vào các bài toán thực tế (có lời giải)
-
13 câu Trắc nghiệm Tích của vectơ với một số có đáp án (Thông hiểu)
-
16 câu Trắc nghiệm Toán 10 Kết nối tri thức Mệnh đề có đáp án
-
Bộ 2 Đề kiểm tra giữa học kì 2 Toán 10 Kết nối tri thức có đáp án - Đề 1
-
10 Bài tập Tính số trung bình, trung vị, tứ phân vị và mốt của mẫu số liệu cho trước (có lời giải)
-
185 câu Trắc nghiệm Toán 10 Bài 1:Phương trình đường thẳng trong mặt phẳng oxy có đáp án (Mới nhất)
-
15 câu Trắc nghiệm Toán 10 chân trời sáng tạo Không gian mẫu và biến cố có đáp án
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận