PHẦN II. TỰ LUẬN
Động đất hay địa chấn là sự rung chuyển trên bề mặt Trái Đất do kết quả của sự giải phóng năng lượng bất ngờ ở lớp vỏ Trái Đất và phái sinh ra sóng địa chấn (theo Wikipedia).
Ngày 6/2/2023, một trận động đất cường độ 7,8 độ richter có tâm chấn tại Thổ Nhĩ Kì được mô tả bởi tâm \(I\) của đường tròn tác động \(\left( C \right)\) trong mặt phẳng tọa độ \(Oxy\) (đơn vị trên hai trục tọa độ là km). Biết rằng đường tròn tác động \(\left( C \right)\) đi qua hai thành phố Kahramamaras và Nurdagi được mô tả bởi hai điểm \(K\left( { - 3;10} \right)\) và \(N\left( {8;0} \right)\); tâm chấn \(I\) có hoành độ dương và cách thành phố Aleppo của Syria được mô tả bởi điểm \(G\left( {9; - \frac{{17}}{4}} \right)\) là \(4\sqrt {10} \) km. Tìm bán kính (km) của đường tròn \(\left( C \right)\) (kết quả làm tròn đến hàng phần trăm).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
Giả sử đường tròn tác động \(\left( C \right)\) có phương trình: \({x^2} + {y^2} - 2ax - 2by + c = 0\) với \(I\left( {a;b} \right)\).
Vì \(\left( C \right)\) đi qua hai điểm \(K\left( { - 3;10} \right)\) và \(N\left( {8;0} \right)\) nên ta có \(\left\{ \begin{array}{l}6a - 20b + c = - 109\\ - 16a + c = - 64\end{array} \right.\) (1).
Lại có \(IG = 4\sqrt {10} \) nên \({\left( {9 - a} \right)^2} + {\left( { - \frac{{17}}{4} - b} \right)^2} = 160\) (2).
Từ \(\left\{ \begin{array}{l}6a - 20b + c = - 109\\ - 16a + c = - 64\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = \frac{{c + 64}}{{16}}\\b = \frac{{11c}}{{160}} + \frac{{133}}{{20}}\end{array} \right.\) thay vào (2), ta được
\[{\left( {9 - \frac{{c + 64}}{{16}}} \right)^2} + {\left( { - \frac{{17}}{4} - \frac{{11c}}{{160}} - \frac{{133}}{{20}}} \right)^2} = 160\]\( \Leftrightarrow {\left( {5 - \frac{c}{{16}}} \right)^2} + {\left( {\frac{{109}}{{10}} + \frac{{11c}}{{160}}} \right)^2} = 160\)
\( \Leftrightarrow 25 - \frac{{10}}{{16}}c + \frac{{{c^2}}}{{256}} + \frac{{11881}}{{100}} + \frac{{1199}}{{800}}c + \frac{{121}}{{25600}}{c^2} = 160\)\( \Leftrightarrow \frac{{221}}{{25600}}{c^2} + \frac{{699}}{{800}}c - \frac{{1619}}{{100}} = 0\)
\( \Leftrightarrow c = 16\) hoặc \(c = \frac{{ - 25904}}{{221}}\).
Vì \(I\) có hoành độ dương nên \(c = 16\). Suy ra \(\left\{ \begin{array}{l}a = 5\\b = \frac{{31}}{4}\end{array} \right.\).
Do đó bán kính của đường tròn \(\left( C \right)\) là \(R = \sqrt {{5^2} + {{\left( {\frac{{31}}{4}} \right)}^2} - 16} \approx 8,31\) km.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Hướng dẫn giải
Trả lời: 3,75
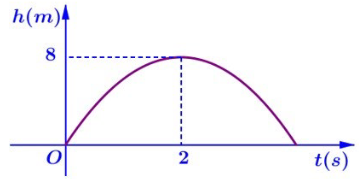
Quỹ đạo của quả bóng là một phần parabol có dạng: \(h\left( t \right) = a{t^2} + bt\).
Khi \(t = 2\) quả bóng lên đến vị trí cao nhất là 8m.
Suy ra \(\left\{ \begin{array}{l} - \frac{b}{{2a}} = 2\\4a + 2b = 8\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}4a + b = 0\\4a + 2b = 8\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}a = - 2\\b = 8\end{array} \right.\). Do đó \(h\left( t \right) = - 2{t^2} + 8t\).
Khi \(h = 1,875\) thì \( - 2{t^2} + 8t = 1,875\)\( \Leftrightarrow t = 0,25\) hoặc \(t = 3,75\).
Vậy khi \(t = 3,75\) giây thì độ cao của quả bóng khi rơi xuống bằng 1,875 m.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Hướng dẫn giải
a) Đ, b) Đ, c) S, d) Đ
a) Số phần tử của không gian mẫu bằng \(C_{12}^5\).
b) Để lấy được 5 viên bi cùng màu thì 5 viên bi lấy được có màu xanh.
Do đó số phần tử của biến cố “5 viên bi lấy ra cùng màu” là \(C_6^5\).
c) Xác suất của biến cố “5 viên bi lấy ra không có bi vàng” là \(P = \frac{{C_{10}^5}}{{C_{12}^5}} = \frac{7}{{22}}\).
d) Xác suất của biến cố “5 viên bi lấy ra có ít nhất một bi vàng” là \(P = 1 - \frac{7}{{22}} = \frac{{15}}{{22}}\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \(\left( { - \infty ;1} \right)\).
B. \(\left( {1; + \infty } \right)\).
C. \(\left( { - \infty ;2} \right)\).
D. \(\left( { - 2; + \infty } \right)\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \(x = - 2\).
B. \(x = - 6\).
C. \(x = - 8\).
D. \(x = - 4\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập