Câu hỏi:
11/03/2025 163
(0,5 điểm) Xét các hình hộp chữ nhật có thể tích bằng \(27\,{\rm{c}}{{\rm{m}}^{\rm{3}}}\) mà đáy là hình vuông cạnh \(a\,\,({\rm{cm}})\) và chiều cao \(h\,\,({\rm{cm}}).\) Tìm hình hộp có diện tích toàn phần nhỏ nhất.
(0,5 điểm) Xét các hình hộp chữ nhật có thể tích bằng \(27\,{\rm{c}}{{\rm{m}}^{\rm{3}}}\) mà đáy là hình vuông cạnh \(a\,\,({\rm{cm}})\) và chiều cao \(h\,\,({\rm{cm}}).\) Tìm hình hộp có diện tích toàn phần nhỏ nhất.
Quảng cáo
Trả lời:
Giải bởi Vietjack
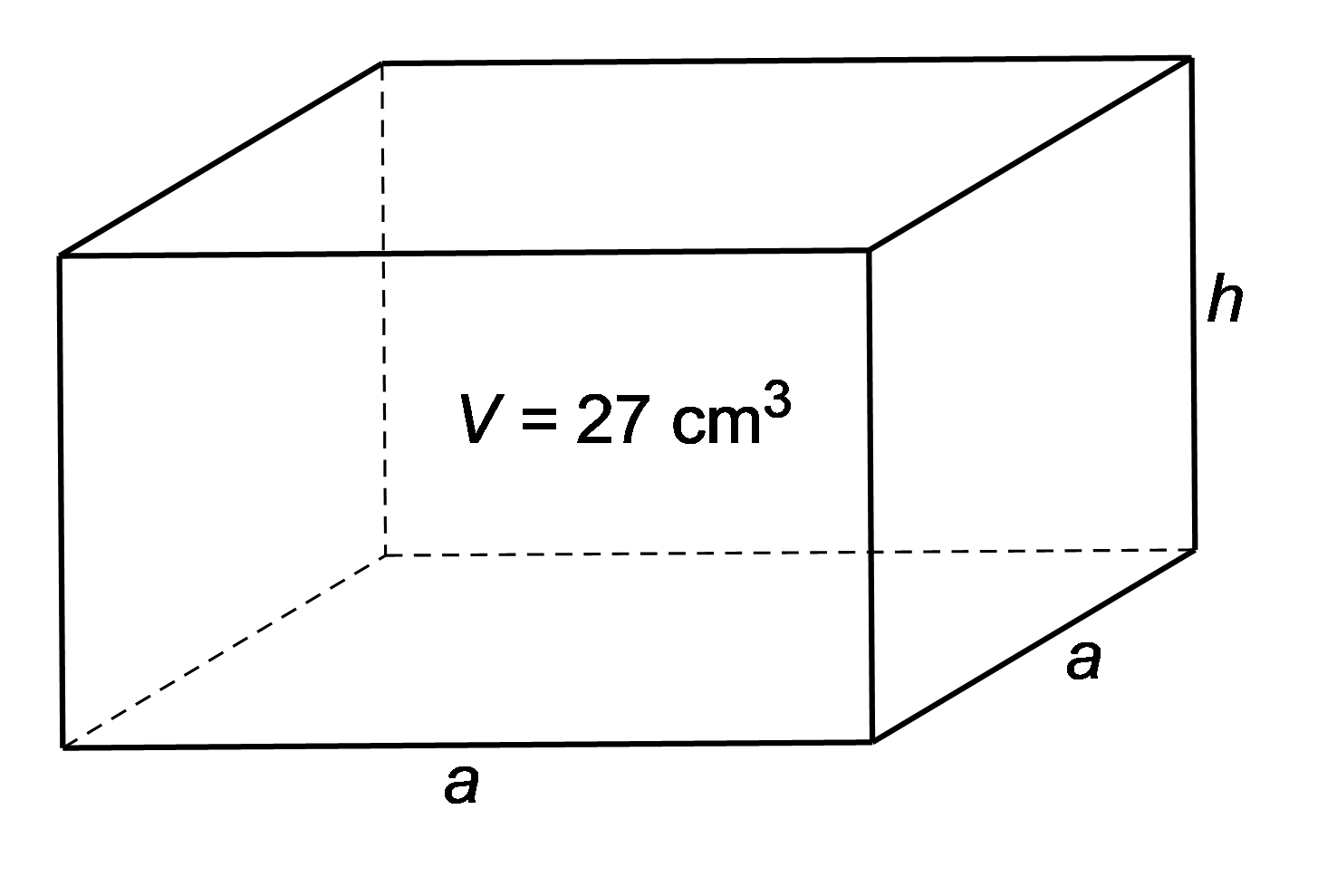
Thể tích của hình hộp chữ nhật là:
\(V = a \cdot a \cdot h = {a^2}h{\rm{\;(c}}{{\rm{m}}^3}{\rm{)}}{\rm{.}}\)
Theo bài, hình hộp chữ nhật có thể tích bằng \(27\,{\rm{c}}{{\rm{m}}^{\rm{3}}}\) nên ta có \({a^2}h = 27,\) suy ra \(h = \frac{{27}}{{{a^2}}}.\)Diện tích toàn phần của hình hộp là:
\({S_{tp}} = {S_{xq}} + 2{S_d} = 4ah + 2{a^2}\)
\( = 4a \cdot \frac{{27}}{{{a^2}}} + 2{a^2} = \frac{{108}}{a} + 2{a^2} = 2\left( {{a^2} + \frac{{27}}{a} + \frac{{27}}{a}} \right)\)
\( \ge 2 \cdot 3\sqrt[3]{{{a^2} \cdot \frac{{27}}{a} \cdot \frac{{27}}{a}}}\) (Bất đẳng thức Cauchy)
\( = 2 \cdot 3 \cdot 9 = 54.\)
Như vậy, \({S_{tp}} \ge 54\). Dấu “=” xảy ra khi và chỉ khi \({a^2} = \frac{{27}}{a}\) hay \(a = 3\) (thỏa mãn \(a > 0).\)
Khi đó, \(h = \frac{{27}}{{{a^2}}} = \frac{{27}}{{{3^2}}} = 3{\rm{\;(cm)}}{\rm{.}}\)
Vậy hình hộp có diện tích toàn phần nhỏ nhất là \(54{\rm{\;c}}{{\rm{m}}^3},\) khi cạnh đáy hình vuông là \(3{\rm{\;cm}}\) và chiều cao là \(3{\rm{\;cm}}.\)
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
a) Nếu người ta làm hàng rào xung quanh công viên thì hàng rào có chiều dài bao nhiêu?
Xem đáp án »
11/03/2025
1,259
Câu 2:
1) Năm ngoái, hai đơn vị sản xuất nông nghiệp thu hoạch được \[600\] tấn thóc. Năm nay, đơn vị thứ nhất làm vượt mức \(10{\rm{\% }}\), đơn vị thứ hai làm vượt mức \(20{\rm{\% }}\) so với năm ngoái. Do đó cả hai đơn vị thu hoạch được \[685\] tấn thóc. Hỏi năm ngoái, mỗi đơn vị thu hoạch được bao nhiêu tấn thóc?
Xem đáp án »
11/03/2025
212
🔥 Đề thi HOT:
-
Dạng 5: Bài toán về lãi suất ngân hàng có đáp án
-
Bộ 10 đề thi cuối kì 1 Toán 9 Kết nối tri thức có đáp án - Đề 01
-
Đề thi minh họa TS vào 10 năm học 2025 - 2026_Môn Toán_Tỉnh Đắk Lắk
-
15 câu Trắc nghiệm Toán 9 Kết nối tri thức Bài 1. Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn có đáp án
-
Dạng 2: Kỹ thuật chọn điểm rơi trong bài toán cực trị xảy ra ở biên có đáp án
-
123 bài tập Nón trụ cầu và hình khối có lời giải
-
Dạng 6: Bài toán về tăng giá, giảm giá và tăng, giảm dân số có đáp án
-
Bộ 10 đề thi cuối kì 2 Toán 9 Chân trời sáng tạo có đáp án (Đề số 1)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận