Câu 9-10: (1,0 điểm) Một quả dưa hấu không hạt ruột đỏ dạng hình cầu có đường kính \[25\,\,{\rm{cm}}\] và phần vỏ dày \[2\,\,{\rm{cm}}.\]
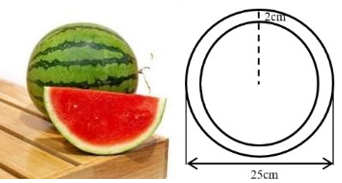
1) Coi phần ruột màu đỏ cũng có dạng hình cầu có cùng tâm với quả dưa hấu. Tính thể tích phần ruột quả dưa hấu.(Kết quả làm tròn đến hàng phần trăm của \[{\rm{c}}{{\rm{m}}^{\rm{3}}}).\]
Câu 9-10: (1,0 điểm) Một quả dưa hấu không hạt ruột đỏ dạng hình cầu có đường kính \[25\,\,{\rm{cm}}\] và phần vỏ dày \[2\,\,{\rm{cm}}.\]
Quảng cáo
Trả lời:
Giải bởi Vietjack
Bán kính của phần ruột quả dưa hấu là: \(\frac{{25 - 2 \cdot 2}}{2} = 10,5\,\,\left( {{\rm{cm}}} \right).\)
Thể tích phần ruột của quả dưa hấu là: \(V = \frac{4}{3}\pi {R^3} = \frac{4}{3}\pi \cdot 10,{5^3} \approx 4\,\,849,05\,\,\left( {{\rm{c}}{{\rm{m}}^3}} \right).\)
Vậy thể tích phần ruột của quả dưa hấu khoảng \(4\,\,849,05\,\,{\rm{c}}{{\rm{m}}^3}.\)
Câu hỏi cùng đoạn
Câu 2:
2) Người ta ép phần ruột màu đỏ của quả dưa hấu trên thì thể tích nước ép thu được bằng 80% thể tích phần ruột. Nước ép dưa hấu sẽ được đựng trong các ly thủy tinh giống nhau, phần lòng trong dạng hình trụ có chiều cao \[10\,\,{\rm{cm}}\] và đường kính đáy lòng trong là \[5\,\,{\rm{cm}}.\] Mỗi ly chỉ chứa được \[70\% \] thể tích. Hỏi để đựng nước ép của quả dưa hấu nói trên thì cần ít nhất bao nhiêu cái ly?
Biết công thức tính thể tích hình trụ là \[V = p{R^2}h\,\,(R\] là bán kính đáy, \(h\)là chiều cao); công thức tính thể tích hình cầu là \[V = \frac{4}{3}p{R^3}\,\,(R\] là bán kính hình cầu).
2) Người ta ép phần ruột màu đỏ của quả dưa hấu trên thì thể tích nước ép thu được bằng 80% thể tích phần ruột. Nước ép dưa hấu sẽ được đựng trong các ly thủy tinh giống nhau, phần lòng trong dạng hình trụ có chiều cao \[10\,\,{\rm{cm}}\] và đường kính đáy lòng trong là \[5\,\,{\rm{cm}}.\] Mỗi ly chỉ chứa được \[70\% \] thể tích. Hỏi để đựng nước ép của quả dưa hấu nói trên thì cần ít nhất bao nhiêu cái ly?
Biết công thức tính thể tích hình trụ là \[V = p{R^2}h\,\,(R\] là bán kính đáy, \(h\)là chiều cao); công thức tính thể tích hình cầu là \[V = \frac{4}{3}p{R^3}\,\,(R\] là bán kính hình cầu).
Giải bởi Vietjack
Thể tích nước ép dưa hấu là: \[{V_n} = \;80\% \cdot 4\,\,849,05 = \;3\,\,879,24\,\,\left( {{\rm{c}}{{\rm{m}}^{\rm{3}}}} \right)\]
Thể tích của phần đựng nước ly thuỷ tinh là:
\[{V_l} = 70\% \cdot \pi {R^2}h = 70\% \cdot \pi \cdot {\left( {\frac{5}{2}} \right)^2} \cdot 10 \approx 137,44\,\,\left( {{\rm{c}}{{\rm{m}}^{\rm{3}}}} \right)\]
Ta có \[\frac{{{V_n}}}{{{V_l}}} \approx \frac{{\;3\,\,879,24}}{{137,44}} \approx 28,22\].
Do đó cần ít nhất 29 cái ly để đựng hết nước ép của quả dưa hấu.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
1) Phương trình \[2{x^2} - 5x + 1 = 0\] có \[a = 2\,;\,\,b = - 5\,;\,\,c = 1\] nên ta có:
\[\Delta \; = \;{\left( { - 5} \right)^2} - \;4 \cdot 2 \cdot 1 = \;25 - \;8 = \;17 > \;0\] nên phương trình có hai nghiệm phân biệt.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
1) Chiều rộng của khu vườn hình chữ nhật sau khi mở rộng là:
\[30 + x + x = 30 + 2x\,\,\left( {\rm{m}} \right)\]
Chiều dài của khu vườn hình chữ nhật sau khi mở rộng là:
\[70 + x + x = 70 + 2x\,\,\left( {\rm{m}} \right)\]
Diện tích của khu vườn hình chữ nhật sau khi mở rộng là:
\[\left( {30 + 2x} \right)\left( {70 + 2x} \right)\,\,\left( {{{\rm{m}}^{\rm{2}}}} \right)\]
Vậy biểu thức \[S\] biểu diễn theo \[x\] là \[S = \left( {30 + 2x} \right)\left( {70 + 2x} \right)\].
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập