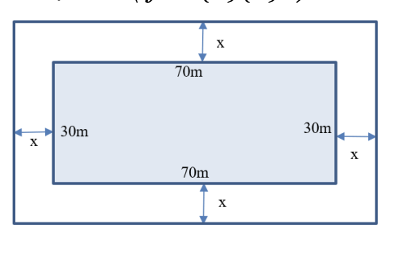
b) Giả sử trong thùng có chứa nước, mực nước chiếm hai phần ba chiều cao của thùng. Tính thể tích nước có trong chiếc thùng đó.
Quảng cáo
Trả lời:
Thể tích nước có trong thùng là:
\(V = \pi \cdot {R^2} \cdot \frac{2}{3}h = \pi \cdot {\left( {0,1} \right)^2} \cdot \frac{2}{3} \cdot 0,6 = 0,004\pi \) (m3).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
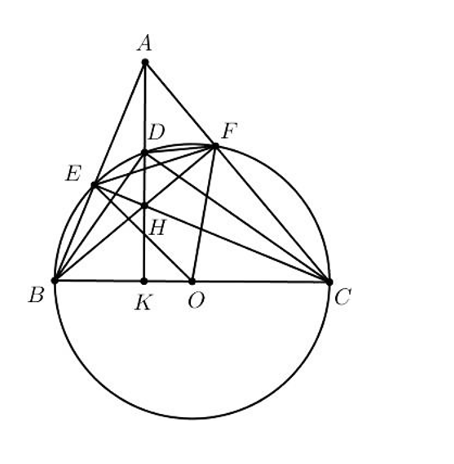
1) Vì \[\widehat {BEC},\,\,\widehat {BFC}\] là các góc nội tiếp chắn nửa đường tròn \(\left( O \right)\) nên ta co
Khi đó \[\Delta AEH\] vuông tại \[E\] nên \[A,\,\,E,\,\,H\] cùng thuộc đường tròn đường kính \[AH.\]
Tương tự \[\Delta AFH\]vuông tại F nên \[A,\,\,H,\,\,F\] cùng thuộc đường tròn đường kính \[AH.\]Vậy \[A,\,\,E,\,\,F,\,\,H\] cùng thuộc đường trong đường kính \[AH\] hay tứ giác \[AEHF\] nội tiếp.
2) Ta có (tính chất góc nội tiếp chắn nửa đường tròn)
Xét BDK và BCD có \[\widehat {CBD}\] chung; \[\widehat {BKD} = \;\widehat {BDC}\,\,\left( { = \;90^\circ } \right)\]
Do đó
Suy ra \(\frac{{BD}}{{BC}} = \frac{{BK}}{{BD}}\) hay \[B{D^2} = BK \cdot BC\].
Do nên \[\widehat {BDH} = \;\widehat {BCD}\] (hai góc tương ứng).
Mà \[\widehat {BCD} = \widehat {BFD}\] (hai góc nội tiếp cùng chắn cung \[BD)\]
Nên \[\widehat {BDH} = \widehat {BFD}\] (đpcm)
Do \[\Delta AFB\] vuông tại \[F\] nên \[\widehat {ABF} = 90^\circ - \widehat {BAF} = 90^\circ - 60^\circ = 30^\circ \].
Mà nên \[\widehat {OEF} = 2 \cdot 30^\circ = 60^\circ .\]
Xét \[\Delta OEF\] cân tại \[O\] (do \[OE = OF\]) có \[\widehat {EOF} = 60^\circ \] nên \[\Delta OEF\] là tam giác đều.
Suy ra \[EF = OE = OF = \frac{1}{2}BC = 3\,\,{\rm{cm}}{\rm{.}}\]
Xét \[\Delta ABC\] có đường cao \[CE\] và \[BF\] cắt nhau tại \[H\] nên \[H\] là trực tâm.
Suy ra \[AH \bot BC\]
Xét \[\Delta AHF\] và \[\widehat {BHK}\] có \[\widehat {AHF} = \;\widehat {BHK}\] (đối đỉnh) và \[\widehat {AFH} = \;\widehat {BKH}\,\,\left( { = \;90^\circ } \right)\]
Suy ra \[\widehat {HAF} = \widehat {HBK}\] hay \[\widehat {HAF} = \widehat {FBC}\]
Kết hợp \[\widehat {AFH} = \;\widehat {BFC}\,\,\left( { = \;90^\circ } \right)\] suy ra
Suy ra \(\frac{{AH}}{{BC}} = \frac{{AF}}{{BF}} = \cot \widehat {FAB} = \cot 60^\circ = \frac{{\sqrt 3 }}{3}\) .
Suy ra \(AH = \frac{{\sqrt 3 }}{3} \cdot BC = \frac{{\sqrt 3 }}{3} \cdot 6 = 2\sqrt 3 .\)
Xét tứ giác \[AEHF\] nội tiếp đường tròn đường kính \[AH\] nên bán kính bằng \(\frac{{2\sqrt 3 }}{2} = \sqrt 3 .\)
Vậy \[EF = 3\,\,{\rm{cm}}\] và bán kính đường tròn ngoại tiếp tam giác \[AEF\] là \(\sqrt 3 .\)
Lời giải
1) Gọi \[a\] là số tấn hợp kim thép chứa \[10\% \] crom cần dùng \[\left( {a > 0} \right).\]
Khi đó, \[500--a\] là số tấn hợp kim thép 30% cần dùng.
Ta có \[a \cdot 10\% + \left( {500--a} \right) \cdot 30\% = 500 \cdot 16\% \]
\[10a + \left( {500--a} \right) \cdot 30 = 500 \cdot 16\]
\[a + 1\,\,500--3a = 800\]
\[2a = 700\]
\[a = 350\] (TMĐK)
Vậy số hợp kim thép chứa \[10\% \] crom cần dùng là 350 tấn, số hợp kim thép chứa \[30\% \] cần dùng là 150 tấn.
2) Số crôm từ 100 tấn thép chứa \[10\% \] crôm là \[10\% \cdot 100 = 10\] (tấn)
Số crôm từ x tấn thép chứa 30% crôm là \[0,3x\] (tấn)
Tổng số tấn thép là \[100 + x\] (tấn)
Phần trăm crôm có trong tổng số tấn thép nhà máy dự định luyện ra là: \(\frac{{10 + 0,3x}}{{100 + x}} \cdot 100\,\,\left( \% \right)\)
Theo đầu bài, thép không gỉ Ferritic có chứa từ 12 đến 27 phần trăm crôm, ta có:
\(12 \le \frac{{10 + 0,3x}}{{100 + x}} \cdot 100 \le 27\)
\(1\,\,200 + 12x \le 1\,\,000 + 30x \le 2\,\,700 + 27x\)
|
Xét \[1\,\,200 + 12x \le 1\,\,000 + 30x\] \[30x - 12x \ge 1\,\,200 - 1\,\,000\] \[18x \ge 200\] \[x \ge \frac{{100}}{9} & \left( 1 \right)\] |
Xét \[1\,\,000 + 30x \le 2\,\,700 + 27x\] \[30x - 27x \le 2\,\,700 - 1\,\,000\] \[3x \le 1\,\,700\] \[x \le \frac{{1\,\,700}}{3} & \left( 2 \right)\] |
Từ \[\left( 1 \right)\] và \[\left( 2 \right)\] suy ra \[\frac{{100}}{9} \le x \le \frac{{1\,\,700}}{3}.\]
Vậy \[x\] nằm trong khoảng \[\frac{{100}}{9}\] đến \[\frac{{1\,\,700}}{3}.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
![Một quả dưa hấu không hạt ruột đỏ dạng hình cầu có đường kính 25cm và phần vỏ dày 2 cm] (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/anh-man-hinh-2025-10-24-luc-200412-1761310950.png)