Số đối của \(A = \sqrt[3]{{ - 8}} - \sqrt {{{\left( {1 - \sqrt 2 } \right)}^2}} \) là
Quảng cáo
Trả lời:
Đáp án đúng là: A
Ta có: \(A = \sqrt[3]{{ - 8}} - \sqrt {{{\left( {1 - \sqrt 2 } \right)}^2}} = \sqrt[3]{{{{\left( { - 2} \right)}^3}}} - \left| {1 - \sqrt 2 } \right| = - 2 - \left( {\sqrt 2 - 1} \right) = - 2 - \sqrt 2 + 1 = - \sqrt 2 - 1.\)
Như vậy, số đối của \(A\) là \( - A = - \left( { - \sqrt 2 - 1} \right) = \sqrt 2 + 1.\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Để đồ thị của hàm số \(y = \left( {m - 1} \right){x^2}\,\,\left( {m \ne 1} \right)\) đi qua điểm \(A\left( { - 1;2} \right)\) thì tọa độ điểm \(A\) thỏa mãn hàm số đó.
Thay \(x = - 1,\,\,y = 2\) vào hàm số \(y = \left( {m - 1} \right){x^2},\) ta được:
\(2 = \left( {m - 1} \right) \cdot {\left( { - 1} \right)^2}\) hay \(m - 1 = 2,\) nên \(m = 3\) (thỏa mãn).
Vậy \(m = 3.\)
Câu 2
Lời giải
![Cho tam giác đều \[MNP\] nội tiếp đường tròn \(\left( O \right)\) như hình vẽ. Phép quay ngược chiều \(240^\circ \) tâm \[O\] biến các điểm \(N,\,\,M,\,\,P\) thành các điểm (ảnh 2)](https://video.vietjack.com/upload2/quiz_source1/2025/03/13-1741763442.png)
Hướng dẫn giải
Đáp án đúng là: C
Các cung \(MN,\,\,NP,\,\,PM\) chia đường tròn \(\left( O \right)\) thành ba cung có số đo bằng nhau, suy ra mỗi cung có số đo bằng \[\frac{{360^\circ }}{3} = 120^\circ .\]
Phép quay ngược chiều \(240^\circ \) tâm \[O\] biến các điểm \(N,\,\,M,\,\,P\) thành các điểm \(M,\,\,P,\,\,N.\)Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
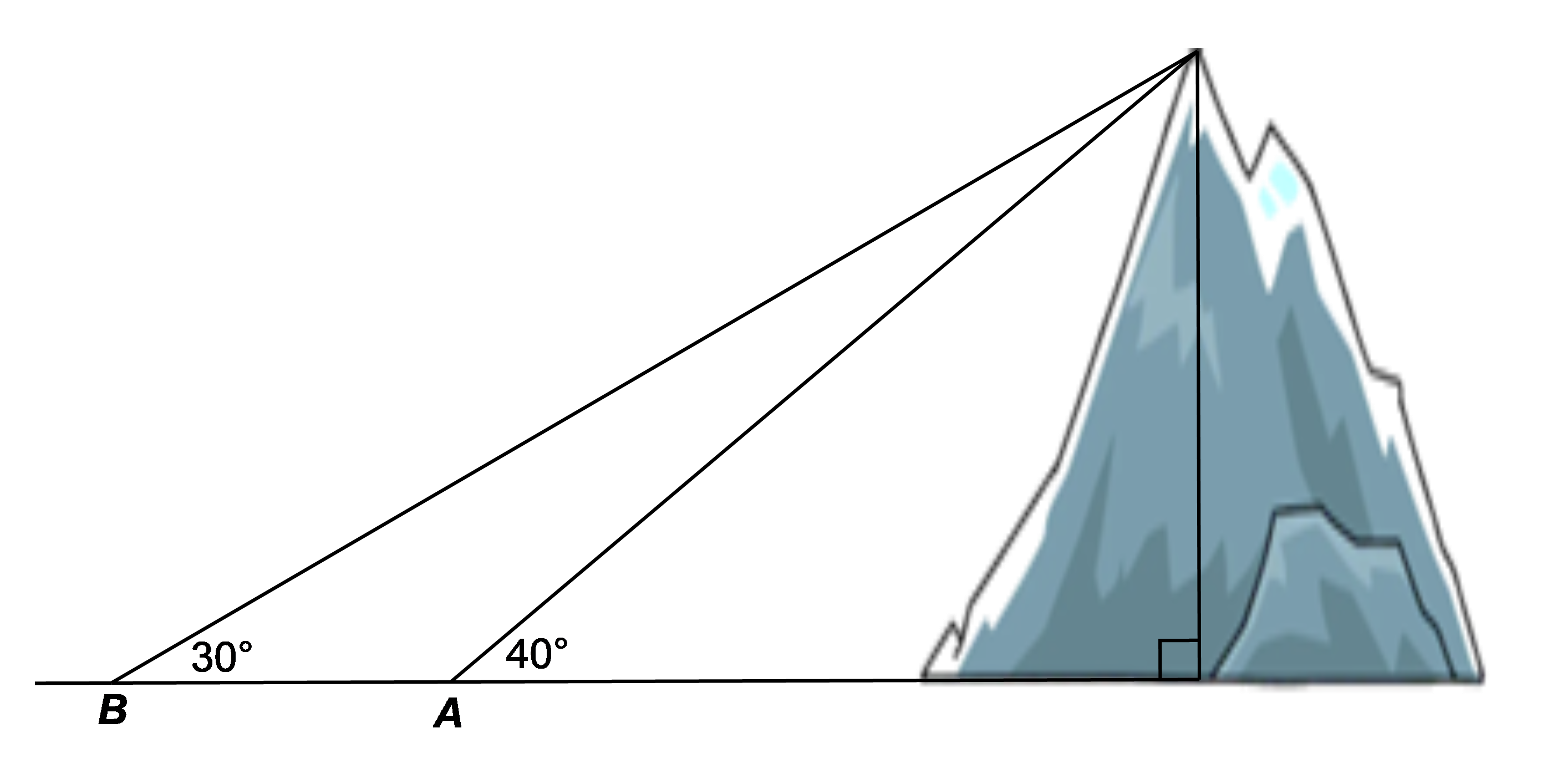
A. 1 110 m.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
![Cho tam giác đều \[MNP\] nội tiếp đường tròn \(\left( O \right)\) như hình vẽ. Phép quay ngược chiều \(240^\circ \) tâm \[O\] biến các điểm \(N,\,\,M,\,\,P\) thành các điểm (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/03/12-1741763486.png)