II. PHẦN TỰ LUẬN (7,0 điểm)
Câu 21-23. (2,5 điểm)
1) Tìm tham số \(m\) để đồ thị của hàm số \(y = \left( {m - 1} \right){x^2}\,\,\left( {m \ne 1} \right)\) đi qua điểm \(A\left( { - 1;2} \right)\).
II. PHẦN TỰ LUẬN (7,0 điểm)
Câu 21-23. (2,5 điểm)
Quảng cáo
Trả lời:
Để đồ thị của hàm số \(y = \left( {m - 1} \right){x^2}\,\,\left( {m \ne 1} \right)\) đi qua điểm \(A\left( { - 1;2} \right)\) thì tọa độ điểm \(A\) thỏa mãn hàm số đó.
Thay \(x = - 1,\,\,y = 2\) vào hàm số \(y = \left( {m - 1} \right){x^2},\) ta được:
\(2 = \left( {m - 1} \right) \cdot {\left( { - 1} \right)^2}\) hay \(m - 1 = 2,\) nên \(m = 3\) (thỏa mãn).
Vậy \(m = 3.\)
Câu hỏi cùng đoạn
Câu 2:
2) Rút gọn biểu thức \(A = \left( {\frac{{\sqrt x }}{{\sqrt x - 2}} - \frac{2}{{\sqrt x + 2}} + \frac{{4\sqrt x }}{{4 - x}}} \right):\frac{{\sqrt x - 2}}{{\sqrt x }}\) với \(x > 0;x \ne 4\).
Với \(x > 0,\,\,x \ne 4,\) ta có:
\(A = \left( {\frac{{\sqrt x }}{{\sqrt x - 2}} - \frac{2}{{\sqrt x + 2}} + \frac{{4\sqrt x }}{{4 - x}}} \right):\frac{{\sqrt x - 2}}{{\sqrt x }}\)
\( = \left[ {\frac{{\sqrt x }}{{\sqrt x - 2}} - \frac{2}{{\sqrt x + 2}} - \frac{{4\sqrt x }}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right)}}} \right] \cdot \frac{{\sqrt x }}{{\sqrt x - 2}}\)
\( = \left[ {\frac{{\sqrt x \left( {\sqrt x + 2} \right)}}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right)}} - \frac{{2\left( {\sqrt x - 2} \right)}}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right)}} - \frac{{4\sqrt x }}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right)}}} \right] \cdot \frac{{\sqrt x }}{{\sqrt x - 2}}\)
\( = \frac{{x + 2\sqrt x - 2\sqrt x + 4 - 4\sqrt x }}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right)}} \cdot \frac{{\sqrt x }}{{\sqrt x - 2}}\)
\( = \frac{{x - 4\sqrt x + 4}}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right)}} \cdot \frac{{\sqrt x }}{{\sqrt x - 2}}\)
\[ = \frac{{{{\left( {\sqrt x - 2} \right)}^2} \cdot \sqrt x }}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right) \cdot \left( {\sqrt x - 2} \right)}}\]
\[ = \frac{{\sqrt x }}{{\sqrt x + 2}}.\]
Vậy với \(x > 0,\,\,x \ne 4\) thì \(A = \frac{{\sqrt x }}{{\sqrt x + 2}}.\)
Câu 3:
3) Giải bất phương trình sau: \(3 - 4x < 0\).
Giải bất phương trình:
\(3 - 4x < 0\)
\( - 4x < - 3\)
\(x > \frac{3}{4}.\)
Vậy bất phương trình đã cho có nghiệm là \(x > \frac{3}{4}.\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
![Cho tam giác đều \[MNP\] nội tiếp đường tròn \(\left( O \right)\) như hình vẽ. Phép quay ngược chiều \(240^\circ \) tâm \[O\] biến các điểm \(N,\,\,M,\,\,P\) thành các điểm (ảnh 2)](https://video.vietjack.com/upload2/quiz_source1/2025/03/13-1741763442.png)
Hướng dẫn giải
Đáp án đúng là: C
Các cung \(MN,\,\,NP,\,\,PM\) chia đường tròn \(\left( O \right)\) thành ba cung có số đo bằng nhau, suy ra mỗi cung có số đo bằng \[\frac{{360^\circ }}{3} = 120^\circ .\]
Phép quay ngược chiều \(240^\circ \) tâm \[O\] biến các điểm \(N,\,\,M,\,\,P\) thành các điểm \(M,\,\,P,\,\,N.\)Câu 2
Lời giải
Đáp án đúng là: B
Kí hiệu 4 học sinh nam lần lượt là X1, X2, X3, X4 và 2 học sinh nữ lần lượt là Y1, Y2.
Không gian mẫu của phép thử là:
\(\Omega = \){X1X2; X1X3; X1X4; X2X3; X2X4; X3X4; Y1Y2; X1Y1; X1Y2; X2Y1; X2Y2; X3Y1; X3Y2; X4Y1; X4Y2}.
Không gian mẫu có 15 phần tử.
Gọi A là biến cố: “Hai học sinh được chọn có ít nhất một học sinh nữ”.
Có 9 kết quả thuận lợi cho biến cố A là: Y1Y2; X1Y1; X1Y2; X2Y1; X2Y2; X3Y1; X3Y2; X4Y1; X4Y2.
Xác suất của biến cố A là: \(\frac{9}{{15}} = \frac{3}{5}.\)
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
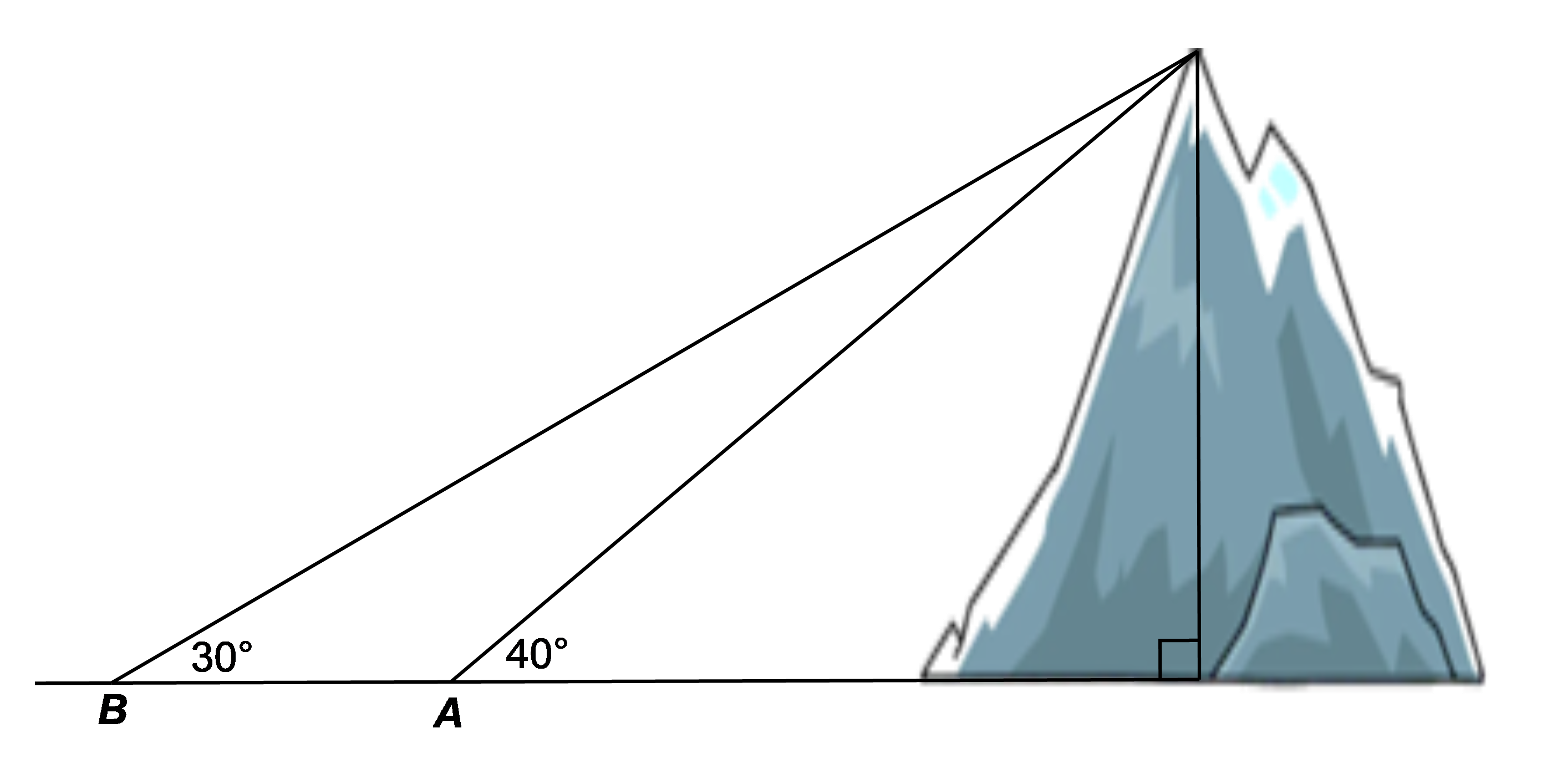
A. 1 110 m.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
![Cho tam giác đều \[MNP\] nội tiếp đường tròn \(\left( O \right)\) như hình vẽ. Phép quay ngược chiều \(240^\circ \) tâm \[O\] biến các điểm \(N,\,\,M,\,\,P\) thành các điểm (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/03/12-1741763486.png)