Câu hỏi:
12/03/2025 68
Cho tam giác \[ABC\] vuông tại \[A,\,\,BC = a,\,\,\,AC = b,\,\,\,AB = c.\] Khẳng định nào dưới đây đúng?
Quảng cáo
Trả lời:
Giải bởi Vietjack
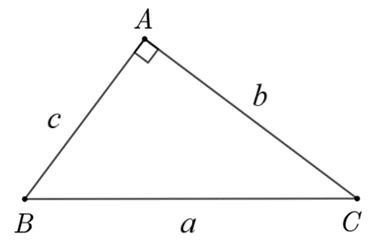
Đáp án đúng là: C
Tam giác \[ABC\] vuông tại \[A\] có
\[b = a \cdot \sin C = c \cdot \tan C.\]
Vậy khẳng định đúng là \[b = a \cdot \sin B.\]
Sách thầy cô Vietjack biên soạn:
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Vì đồ thị hàm số đi qua điểm \(M\left( {\sqrt 2 \,;\,\,2} \right)\) nên thay \(x = \sqrt 2 \), \(y = 2\) vào hàm số \(y = a{x^2},\) ta được \(2 = a{\left( {\sqrt 2 } \right)^2}\) . Suy ra \(a = 1\).
Vậy \(a = 1\) thì đồ thị hàm số \(y = a{x^2}\) đi qua điểm \(M\left( {\sqrt 2 \,;{\rm{ }}2} \right)\).
b) Ta có \[\Delta \, = \,{\left[ { - \left( {2m\, + \,1} \right)} \right]^2}\, - \,4 \cdot 1\, \cdot \,m\]
\[ = \,\left( {4{m^2}\, + \,4m\, + \,1} \right)\, - \,4m\]\[ = \,\,4{m^2}\, + \,1 > 0\] với mọi \[m \in \mathbb{R}\]
Do đó, phương trình luôn có hai nghiệm phân biệt \({x_1},{x_2}\).
Theo định lí Viète, ta có: \[\left\{ \begin{array}{l}{x_1}\, + \,{x_2}\, = \,2m\, + \,1\\{x_1}{x_2}\, = \,m\end{array} \right.\].
Khi đó: \[\left( {{x_1} - 1} \right)\left( {{x_2} - 1} \right) \ge 19\] hay \({x_1}{x_2} - \left( {{x_1} + {x_2}} \right) + 1 \ge 19\)
Suy ra \(m - \left( {2m + 1} \right) + 1 \ge 19\) hay \(m \le - 19\)
Vậy \(m \le - 19\) thoả mãn yêu cầu đề bài.
Lời giải
Đáp án đúng là: C
Thay \(x = - 1;\,\,y = 2\) vào hàm số \(y = - 2{x^2}\), ta được \( - 2 \cdot {\left( { - 1} \right)^2} - 2 \ne 2\) nên điểm \[\left( { - 1\,;\,\,2} \right)\] không thuộc đồ thị hàm số \(y = - 2{x^2}.\)
Thay \(x = 2\,;\,\,y = - 1\) vào hàm số \(y = - 2{x^2}\), ta được \( - 2 \cdot {2^2} = - 8 \ne - 1\) nên điểm \[\left( { - 1\,;\,\,2} \right)\] không thuộc đồ thị hàm số \(y = - 2{x^2}.\)
Thay \(x = - 1\,;\,\,y = - 2\) vào hàm số \(y = - 2{x^2}\), ta được \( - 2 \cdot {\left( { - 1} \right)^2} = - 2\) nên điểm \[\left( { - 1\,;\,\,2} \right)\] thuộc đồ thị hàm số \(y = - 2{x^2}.\)
Thay \(x = - 2\,;\,\,y = - 1\) vào hàm số \(y = - 2{x^2}\), ta được \[ - 2 \cdot {\left( { - 2} \right)^2} = - 8 \ne 2\] nên điểm \(\left( { - 2\,;\,\, - 1} \right).\) không thuộc đồ thị hàm số \(y = - 2{x^2}.\)
Vậy chọn đáp án C.
![Cho hình vẽ. Số đo của góc \[\widehat {AMB}\] là (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/03/19-1741778194.png)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
123 bài tập Nón trụ cầu và hình khối có lời giải
-
Đề thi minh họa TS vào 10 năm học 2025 - 2026_Môn Toán_Tỉnh Đắk Lắk
-
50 bài tập Một số yếu tố xác suất có lời giải
-
Đề thi tham khảo môn Toán vào 10 tỉnh Quảng Bình năm học 2025-2026
-
Đề thi minh họa TS vào 10 năm học 2025 - 2026_Môn Toán_TP Hà Nội
-
Đề thi minh họa (Dự thảo) TS vào 10 năm học 2025 - 2026_Môn Toán_Tỉnh Đồng Nai
-
Đề thi thử TS vào 10 (Lần 2 - Tháng 2) năm học 2025 - 2026_Môn Toán_THCS Hoằng Thanh_Tỉnh Thanh Hóa
-
Đề thi tham khảo TS vào 10 năm học 2025 - 2026_Môn Toán_Tỉnh Bình Phước
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận