Quảng cáo
Trả lời:
Giải bởi Vietjack
\(A = \sqrt {16} + \sqrt[3]{{27}} = \sqrt {{4^2}} + \sqrt[3]{{{3^3}}} = 4 + 3 = 7.\)
\(B = \sqrt {{{\left( {3 + \sqrt 5 } \right)}^2}} = \left| {3 + \sqrt 5 } \right| = 3 + \sqrt 5 .\)
Câu hỏi cùng đoạn
Câu 2:
2) Rút gọn biểu thức: , với
Giải bởi Vietjack
Với \(x \ne - \sqrt 5 ,\) ta có:
\(P = \frac{{{x^2} - 5}}{{x + \sqrt 5 }} = \frac{{\left( {x + \sqrt 5 } \right)\left( {x - \sqrt 5 } \right)}}{{x + \sqrt 5 }} = x - \sqrt 5 .\)
Vậy với \(x \ne - \sqrt 5 \) thì \(P = x - \sqrt 5 .\)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bảng tần số biểu diễn số lỗi chính tả của học sinh như sau:
|
Số lỗi chính tả |
0 |
1 |
2 |
3 |
4 |
5 |
|
Tần số |
4 |
10 |
7 |
5 |
8 |
6 |
Kích thước mẫu là: \(N = 40.\)
Vì tần số của giá trị 0 là 4 nên tần số tương đối của giá trị 0 là\(\frac{4}{{40}} \cdot 100\% = 10\% .\)
Vì tần số của giá trị 1 là 10 nên tần số tương đối của giá trị 1 là \(\frac{{10}}{{40}} \cdot 100\% = 25\% .\)
Tương tự, ta tính được tần số tương đối của các giá trị 2, 3, 4, 5 lần lượt là \(17,5\% ;\,\,12,5\% ;\,\,20\% ;\,\,15\% .\)
Ta thu được bảng tần số tương đối như sau:
|
Số lỗi chính tả |
0 |
1 |
2 |
3 |
4 |
5 |
|
Tần số tương đối |
\(10\% \) |
\(25\% \) |
\(17,5\% \) |
\(12,5\% \) |
\(20\% \) |
\(15\% \) |
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bảng giá trị của hàm số:
|
\(x\) |
\( - 2\) |
\( - 1\) |
\(0\) |
\(1\) |
\(2\) |
|
\(y = \frac{1}{2}{x^2}\) |
\(2\) |
\(\frac{1}{2}\) |
\(0\) |
\(\frac{1}{2}\) |
\(2\) |
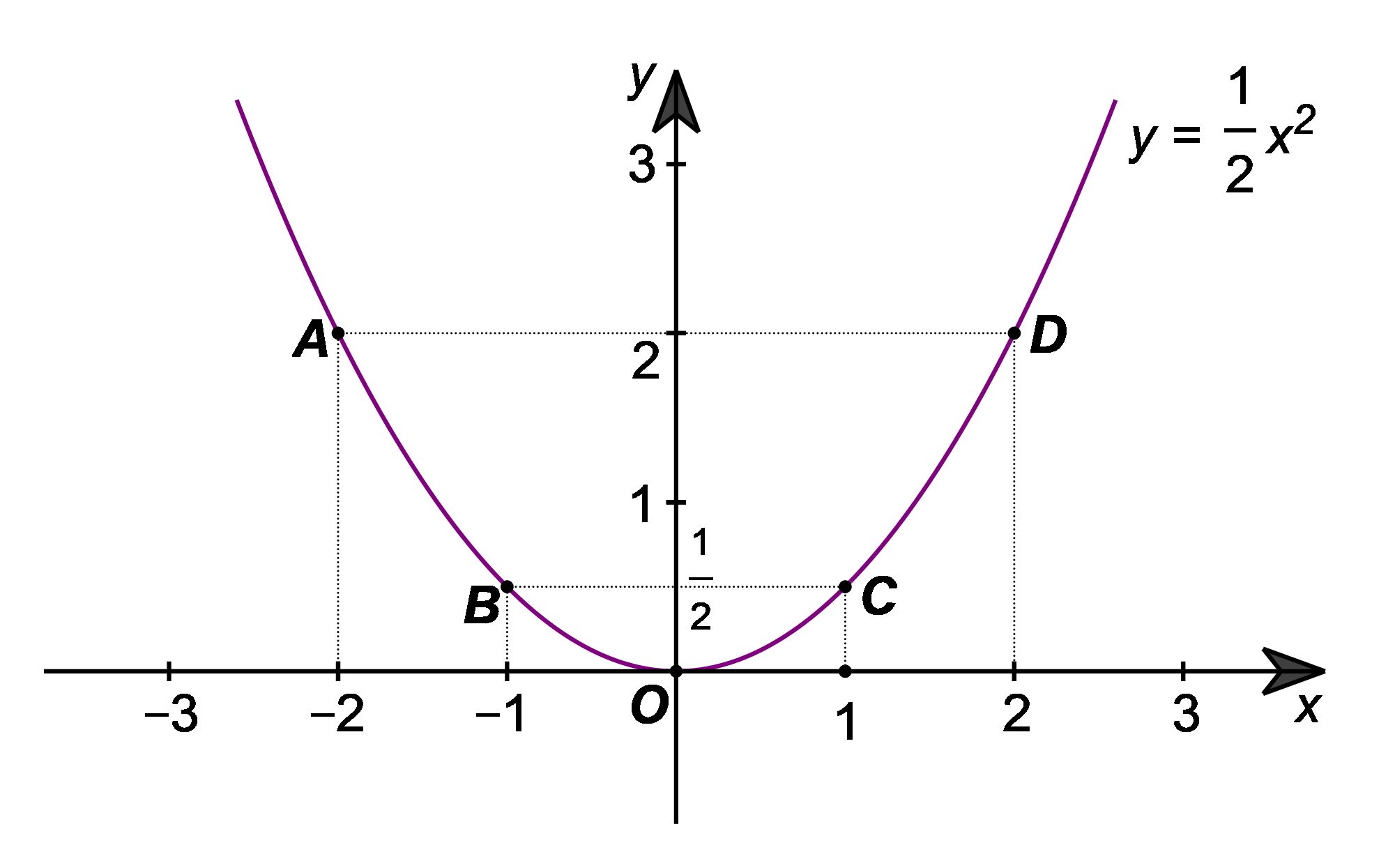
Trên mặt phẳng tọa độ \(Oxy,\) lấy các điểm \(A\left( { - 2;\,\,2} \right),\) \(B\left( { - 1;\,\,\frac{1}{2}} \right),\) \(O\left( {0;\,\,0} \right),\) \(C\left( {1;\,\,\frac{1}{2}} \right),\) \(D\left( {2;\,\,2} \right).\)
Đồ thị của hàm số \(y = \frac{1}{2}{x^2}\) là một đường parabol đỉnh \(O,\) đi qua các điểm trên và có dạng như hình vẽ sau:
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập