Thời g̣ian rơi $t$ tính theo giây của một vật được thả rơi tự do từ độ cao $h(m)$ cho đến khi chạm đất thoả mãn hệ thức $h = 5{t^2}$.

a) Tính thời gian rơi của vật khi $h = 20\;m$ và khi $h = 10\;m$ (kết quả làm tròn đến hàng phần mười của giây).

b) Viết công thức biểu thị thời gian rơi $t$ theo độ cao $h(h > 0)$.

Xem lời giải

Câu hỏi trong đề: 33 bài tập Căn thức có lời giải !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

a) Với $h = 20\;m$ ta có $20 = 5{t^2} \Leftrightarrow {t^2} = 4 \Rightarrow t = 2\left( s \right)\left( {do{\rm{ }}t > 0} \right)$.

Với $h = 10m$ ta có $10 = 5{t^2} \Leftrightarrow {t^2} = 2 \Rightarrow t = \sqrt 2 \approx 1,4\left( s \right)$

b) $h = 5{t^2} \Rightarrow {t^2} = \frac{h}{5} \Rightarrow t = \sqrt {\frac{h}{5}} \left( {do{\rm{ }}t > 0} \right)$

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Để tính toán thời gian một chu kỳ đong đưa (một chu kỳ đong đưa dây đu được tính từ lúc dây đu bắt đầu được đưa lên cao đến khi dừng hẳn) của một dây đu, người ta sử dụng công thức: ${\rm{T}} = 2\pi \sqrt {\frac{{\rm{L}}}{{\rm{g}}}} $. Trong đó, T là thời gian một chu kỳ đong đưa, L là chiều dài của dây đu, ${\rm{g}} = 9,81\;{\rm{m}}/{{\rm{s}}^2}$.

$Một dây đu có chiều dài $2 + \sqrt 3 \;{\rm{m}}$, hỏi chu kỳ đong đưa dài bao nhiêu giây? (ảnh 1)$

a) Một dây đu có chiều dài $2 + \sqrt 3 \;{\rm{m}}$, hỏi chu kỳ đong đưa dài bao nhiêu giây?

b) Một người muốn thiết kế một dây đu sao cho một chu kỳ đong đưa của nó kéo dài 4 giây. Hỏi người đó phải làm một dây đu dài bao nhiêu?

Xem đáp án

Lời giải

a) Thay ${\rm{L}} = 2 + \sqrt 3 ;{\rm{g}} = 9,81$ vào công thức ${\rm{T}} = 2\pi \sqrt {\frac{{\rm{L}}}{{\rm{g}}}} $, ta được:${\rm{T}} = 2\pi \sqrt {\frac{{2 + \sqrt 3 }}{{9,81}}} \approx 3,88{\rm{ (gi\^a y)}}{\rm{. }}$
Vậy chu kỳ đong đưa dài 3,88 giây.
b) Thay ${\rm{T}} = 4;{\rm{g}} = 9,81$ vào công thức ${\rm{T}} = 2\pi \sqrt {\frac{{\rm{L}}}{{\rm{g}}}} $, ta được:
$4 = 2\pi \cdot \sqrt {\frac{{\rm{L}}}{{9,81}}} \Rightarrow \sqrt {\frac{{\rm{L}}}{{9,81}}} = \frac{2}{\pi } \Rightarrow \frac{{\rm{L}}}{{9,81}} = {\left( {\frac{2}{\pi }} \right)^2} \Rightarrow {\rm{L}} = 9,81.{\left( {\frac{2}{\pi }} \right)^2} \approx 4\;{\rm{m}}$
Vậy phải làm một dây đu dài 4 m.

Câu 2

Tốc độ tăng trưởng dân số bình quân hàng năm có thể tính theo công thức: $\overline {\rm{r}} = \sqrt {\frac{{{{\rm{P}}_{\rm{t}}}}}{{{{\rm{P}}_0}}}} - 1$

Trong đó: ${{\rm{P}}_0}$: Dân số thời điểm gốc

${{\rm{P}}_{\rm{t}}}$: Dân số thời điểm năm sau

$\overline {\rm{r}} $: Tốc độ tăng trưởng dân số bình quân hàng năm.

Tổng số dân Việt Nam năm 2014 là 90728,9 ngàn người. Tổng số dân Việt Nam năm 2015 là: 91703,8 ngàn người.

a) Hãy tính tốc độ tăng trưởng dân số bình quân hàng năm của Việt Nam trong giai đoạn trên.

b) Theo tốc độ tăng trưởng trên. Hãy ước tính số dân Việt Nam vào năm 2016.

Xem đáp án

Lời giải

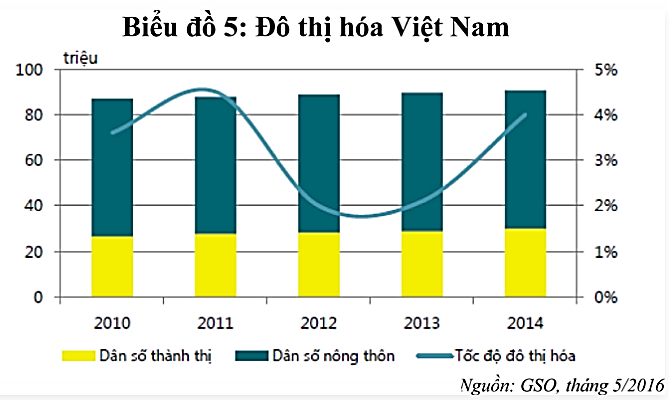
a) Thay ${{\rm{P}}_t} = 91703,8;{{\rm{P}}_0} = 90728,9$ vào công thức $\overline {\rm{r}} = \sqrt {\frac{{{{\rm{P}}_{\rm{t}}}}}{{{{\rm{P}}_0}}}} - 1$, ta được:$\bar r = \sqrt {\frac{{91703,8}}{{90728,9}}} - 1 = 0,0054 = 0,54\% $

Vậy tốc độ tăng trương dân số bình quân hàng năm trong giai đoạn trên của Việt Nam là $0,54\% $.

b) Thay $r = 0,0054;{P_0} = 91703,8$ vào công thức $\bar r = \sqrt {\frac{{{P_t}}}{{{P_0}}}} - 1$, ta được:

$0,054 = \sqrt {\frac{{{{\rm{P}}_{\rm{t}}}}}{{91703,8}}} - 1 \Rightarrow \sqrt {\frac{{{{\rm{P}}_{\rm{t}}}}}{{91703,8}}} = 1,0054 \Rightarrow \frac{{{{\rm{P}}_{\rm{t}}}}}{{91703,8}} = {(1,0054)^2}$

$ \Rightarrow {{\rm{P}}_{\rm{t}}} = {(1,0054)^2} \cdot 91703,8 \approx 92199,00052$

Vậy ước tính số dân Việt Nam vào năm 2016 là 92199,00052 ngàn người.

Câu 3