Vận tốc \({\rm{v}}({\rm{m}}/{\rm{s}})\) của một tàu lượn di chuyển trên một cung tròn có bán kính \({\rm{r}}({\rm{m}})\) được cho bởi công thức: \({\rm{v}} = \sqrt {{\rm{ar}}} \). Trong đó a là gia tốc của tàu \(\left( {{\rm{m}}/{{\rm{s}}^2}} \right)\) (gia tốc là đại lượng vật lý đặc trưng cho sự thay đổi của vận tốc theo thời gian. Nó là một trong những đại lượng cơ bản dùng để mô tả chuyển động và là độ biến thiên của vận tốc theo thời gian).
a) Nếu tàu lượn đang chạy với vận tốc \({\rm{v}} = 14\;{\rm{m}}/{\rm{s}}\) và muốn đạt mức gia tốc tối đa cho phép là \({\rm{a}} = 9\;{\rm{m}}/{{\rm{s}}^2}\) thì bán kính tối thiểu của cung tròn phải là bao nhiêu để xe không văng ra khỏi đường ray?
b) Nếu tàu lượn đang di chuyển với vận tốc \({\rm{v}} = 8\;{\rm{m}}/{\rm{s}}\) xung quanh một cung tròn có bán kính \({\rm{r}} = 25\;{\rm{m}}\) thì có gia tốc tối đa cho phép là bao nhiêu?
Vận tốc \({\rm{v}}({\rm{m}}/{\rm{s}})\) của một tàu lượn di chuyển trên một cung tròn có bán kính \({\rm{r}}({\rm{m}})\) được cho bởi công thức: \({\rm{v}} = \sqrt {{\rm{ar}}} \). Trong đó a là gia tốc của tàu \(\left( {{\rm{m}}/{{\rm{s}}^2}} \right)\) (gia tốc là đại lượng vật lý đặc trưng cho sự thay đổi của vận tốc theo thời gian. Nó là một trong những đại lượng cơ bản dùng để mô tả chuyển động và là độ biến thiên của vận tốc theo thời gian).
a) Nếu tàu lượn đang chạy với vận tốc \({\rm{v}} = 14\;{\rm{m}}/{\rm{s}}\) và muốn đạt mức gia tốc tối đa cho phép là \({\rm{a}} = 9\;{\rm{m}}/{{\rm{s}}^2}\) thì bán kính tối thiểu của cung tròn phải là bao nhiêu để xe không văng ra khỏi đường ray?
b) Nếu tàu lượn đang di chuyển với vận tốc \({\rm{v}} = 8\;{\rm{m}}/{\rm{s}}\) xung quanh một cung tròn có bán kính \({\rm{r}} = 25\;{\rm{m}}\) thì có gia tốc tối đa cho phép là bao nhiêu?
Câu hỏi trong đề: 33 bài tập Căn thức có lời giải !!
Quảng cáo
Trả lời:
a) Thay \({\rm{v}} = 14;{\rm{a}} = 9\) vào công thức \({\rm{v}} = \sqrt {{\rm{ar}}} \), ta được: \(\sqrt {9{\rm{r}}} = 14 \Rightarrow 9{\rm{r}} = 196 \Rightarrow {\rm{r}} = 21,8\;{\rm{m}}\)
Vậy bán kính tối thiểu của cung tròn phải là \(21,8\;{\rm{m}}\).
b) Thay \({\rm{v}} = 8;{\rm{r}} = 25\) vào công thức \({\rm{v}} = \sqrt {{\rm{ar}}} \), ta được: \(\sqrt {25{\rm{a}}} = 8 \Rightarrow 25{\rm{a}} = 64 \Rightarrow {\rm{a}} = 2,56\;{\rm{m}}/{{\rm{s}}^2}\)
Vậy gia tốc tối đa cho phép là \(2,56\;{\rm{m}}/{{\rm{s}}^2}\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
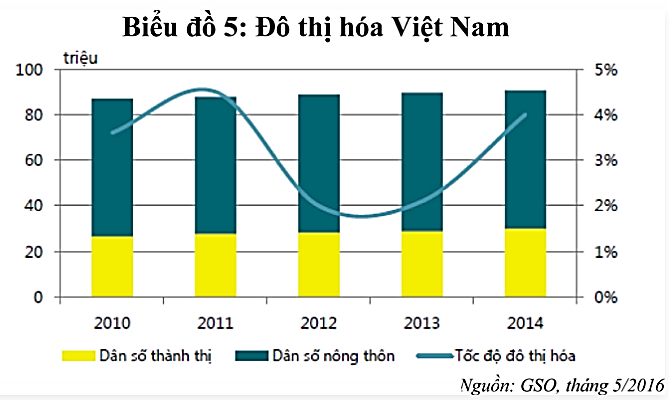
a) Thay \({{\rm{P}}_t} = 91703,8;{{\rm{P}}_0} = 90728,9\) vào công thức \(\overline {\rm{r}} = \sqrt {\frac{{{{\rm{P}}_{\rm{t}}}}}{{{{\rm{P}}_0}}}} - 1\), ta được:\(\bar r = \sqrt {\frac{{91703,8}}{{90728,9}}} - 1 = 0,0054 = 0,54\% \)
Vậy tốc độ tăng trương dân số bình quân hàng năm trong giai đoạn trên của Việt Nam là \(0,54\% \).
b) Thay \(r = 0,0054;{P_0} = 91703,8\) vào công thức \(\bar r = \sqrt {\frac{{{P_t}}}{{{P_0}}}} - 1\), ta được:
\(0,054 = \sqrt {\frac{{{{\rm{P}}_{\rm{t}}}}}{{91703,8}}} - 1 \Rightarrow \sqrt {\frac{{{{\rm{P}}_{\rm{t}}}}}{{91703,8}}} = 1,0054 \Rightarrow \frac{{{{\rm{P}}_{\rm{t}}}}}{{91703,8}} = {(1,0054)^2}\)
\( \Rightarrow {{\rm{P}}_{\rm{t}}} = {(1,0054)^2} \cdot 91703,8 \approx 92199,00052\)
Vậy ước tính số dân Việt Nam vào năm 2016 là 92199,00052 ngàn người.
Lời giải
a) Từ \(W = \frac{1}{2}m{v^2}\), ta có \({v^2} = \frac{{2\;W}}{{\;m}}\), suy ra \(v = \sqrt {\frac{{2\;W}}{{\;m}}} \) (do \(v \ge 0\)).
b) Khi \(m = 0,4\;kg,\;W = 0,5\;J\) thì \(v = \sqrt {\frac{{2.0,5}}{{0,4}}} = \sqrt {\frac{{10}}{4}} = \frac{{\sqrt {10} }}{2}\left( {\;m/s} \right)\). Sử dụng máy tính cầm tay, ta tính được \(v = \frac{{\sqrt {10} }}{2} \approx 1,58\left( {m/s} \right)\).
c) Khi vật có động năng \({{\rm{W}}_1} = 2\;{\rm{W}}\) thì vật có tốc độ \({v_1} = \sqrt {\frac{{2\;{W_1}}}{{\;m}}} = \sqrt {\frac{{2.2\;W}}{{\;m}}} = \sqrt 2 \sqrt {\frac{{2\;W}}{{\;m}}} = v\sqrt 2 \). Suy ra tốc độ của vật tăng gấp \(\sqrt 2 \) lần khi động năng của nó tăng gấp đôi.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.