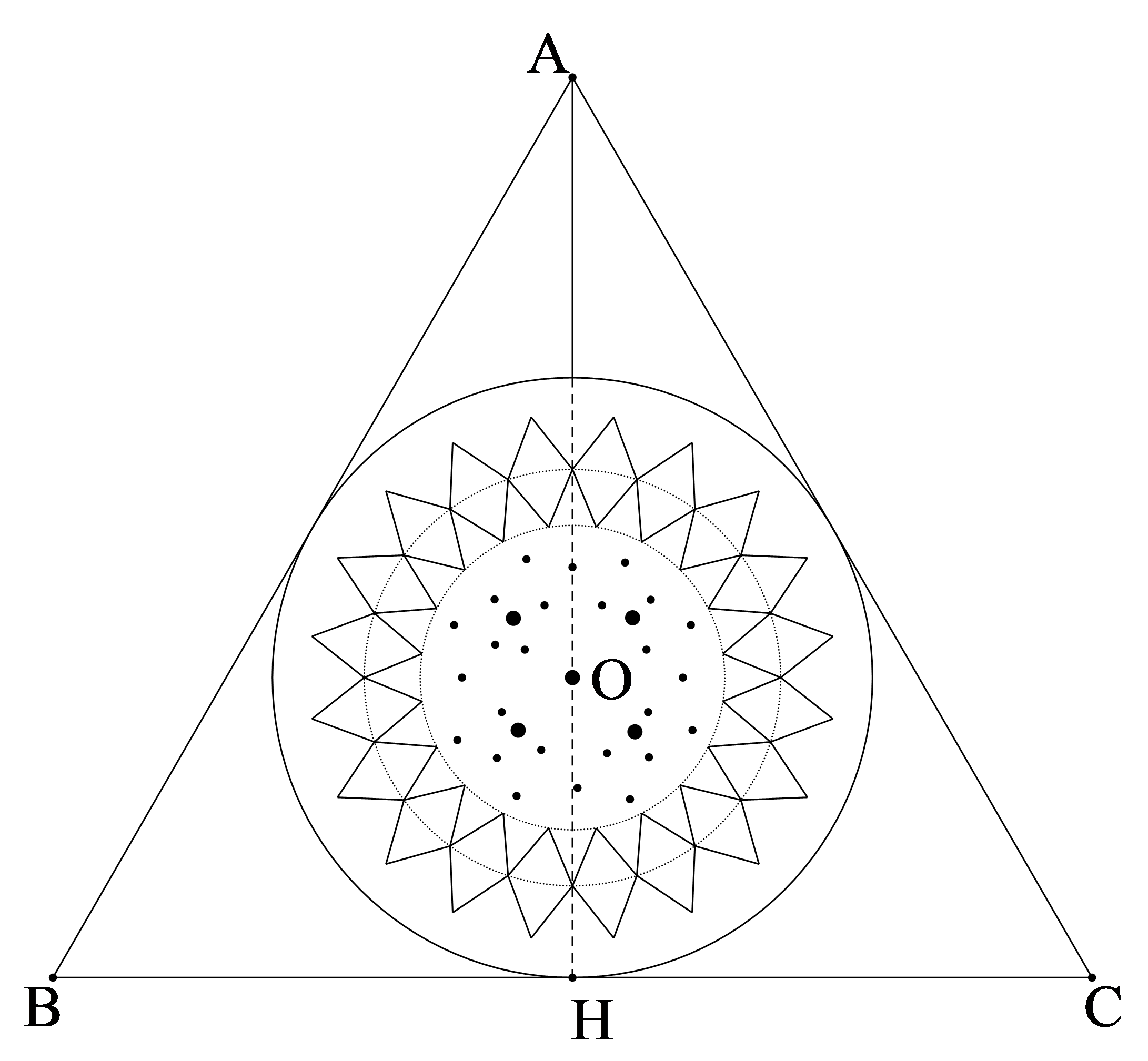Hải đăng Kê Gà tọa lạc tại xã Tân Thành, huyện Hàm Thuận Nam, tỉnh Bình Thuận. Ngọn hải đăng này được người Pháp xây dựng vào tháng 2 năm 1897 và đi vào hoạt động từ năm 1899. Như vậy, đến nay, ngọn hải đăng đã có tuổi đời đến 125 năm. Người thiết kế nên công trình này là kỹ sư người Pháp Chnavat.
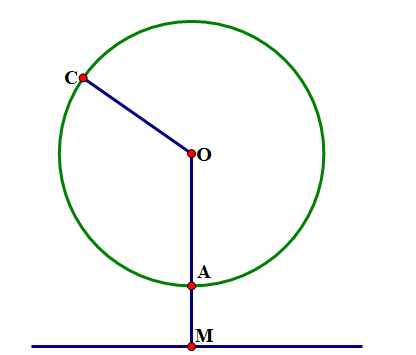
Biết chiều cao ngọn đèn so với bề mặt nước biển là 65 m , bán kính của Trái Đất gần bằng 6400 km và điều kiện quan sát trên biển không bị che khuất thì một người quan sát đứng tại vị trí đèn của ngọn hải đăng thì có thể nhìn xa tối đa bao nhiêu km trên mặt biển (kết quả làm tròn một số thập phân).
Biết chiều cao ngọn đèn so với bề mặt nước biển là 65 m , bán kính của Trái Đất gần bằng 6400 km và điều kiện quan sát trên biển không bị che khuất thì một người quan sát đứng tại vị trí đèn của ngọn hải đăng thì có thể nhìn xa tối đa bao nhiêu km trên mặt biển (kết quả làm tròn một số thập phân).
Câu hỏi trong đề: 62 bài tập Đa giác nội tiếp và đa giác đều có lời giải !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
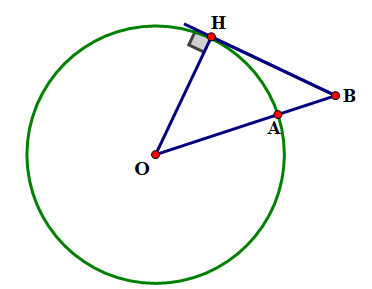
Nên \(BH\) là tiếp tuyến của đường tròn.
Đổi đơn vị: \(65\;{\rm{m}} = 0,065\;{\rm{km}}\).
Ta có \({\rm{OB}} = {\rm{OA}} + {\rm{BA}} = 6400 + 0,065 = 6400,065\;{\rm{km}}\).
Xét \(\Delta {\rm{OBH}}\) vuông tại H , ta có: \({\rm{O}}{{\rm{B}}^2} = {\rm{O}}{{\rm{H}}^2} + {\rm{B}}{{\rm{H}}^2}\) (định lý Pythagore).
Nên \({\rm{BH}} = \sqrt {{\rm{O}}{{\rm{B}}^2} - {\rm{O}}{{\rm{H}}^2}} = \sqrt {6400,{{065}^2} - {{6400}^2}} \approx 28,8(\;{\rm{km}})\).
Vậy tầm nhìn xa nhất người đó có thể nhìn thấy là khoảng \(28,8\;{\rm{km}}\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
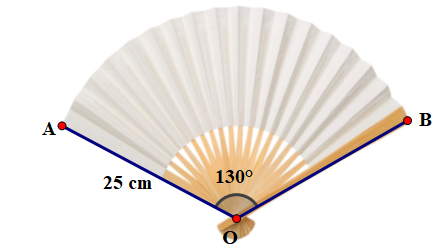
a) Diện tích hình quạt là: \({\rm{S}} = \frac{{\pi {{\rm{R}}^2}{\rm{n}}}}{{360}} = \frac{{\pi \cdot {{25}^2} \cdot 130}}{{360}} \approx 709\left( {\;{\rm{c}}{{\rm{m}}^2}} \right)\).
b) Diện tích giấy làm 100 cây quạt là: \(709 \cdot 2 \cdot 100 = 141800\left( {\;{\rm{c}}{{\rm{m}}^2}} \right)\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
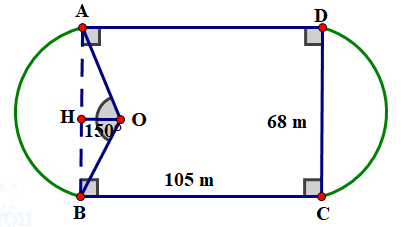
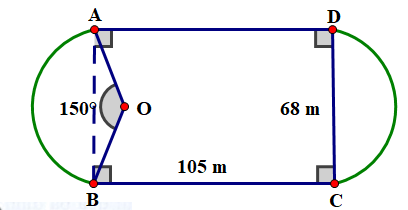
Kẻ \({\rm{OH}} \bot {\rm{AB}}\) tại \(H\), ta có:
Xét vuông tại \(H\), ta có:
Độ dài cung AB là:
Vậy chu vi sân khoảng 394,3 m.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập