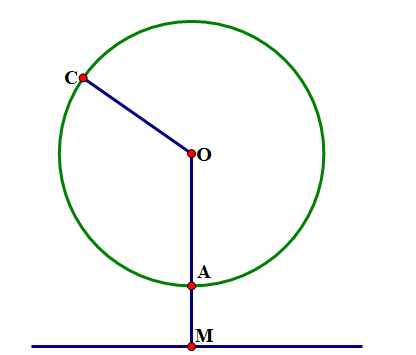
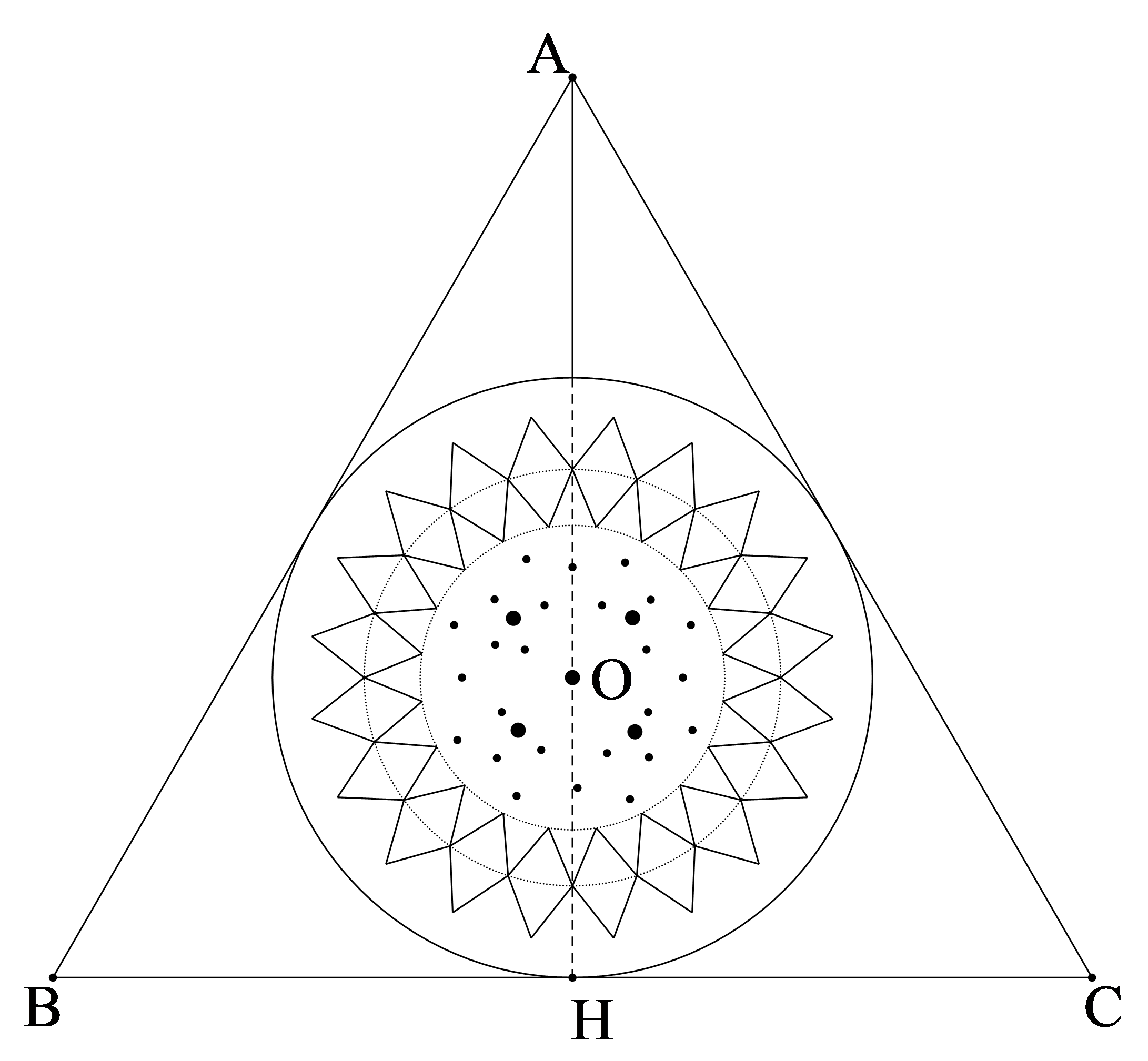Vinasat-1 là vệ tinh địa tĩnh đầu tiên của Việt Nam được phóng vào vũ trụ lúc 22 giờ 17 phút ngày 18 tháng 4 năm 2008. Dự án vệ tinh Vinasat-1 đã khởi hành từ năm 1998 với tổng mức đầu tư khoảng hơn 300 triệu USD. Việt Nam đã tiến hành đàm phán với 27 quốc gia và vùng lãnh thổ để có được vị trí 132 độ Đông trên quỹ đạo địa tĩnh.
Hãy tìm khoảng cách từ vị trí Vinasat-1 (vị trí A ) đến mặt đất (vị trí điểm H ). Biết rằng khi vệ tinh phát ra tín hiệu vô tuyến đến một điểm xa nhất trên mặt đất (vị trí M) thì từ lúc phát tín hiệu đến mặt đất cho đến lúc vệ tinh thu lại được tín hiệu phản hồi mất khoảng thời gian 0,28 giây. Trái Đất được xem như một hình cầu có bán kính khoảng 6400 km . Giả sử vận tốc sóng vô tuyến là \(3 \cdot {10^8}\;{\rm{m}}/{\rm{s}}\).
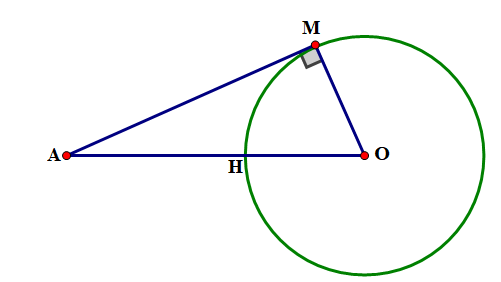
Vinasat-1 là vệ tinh địa tĩnh đầu tiên của Việt Nam được phóng vào vũ trụ lúc 22 giờ 17 phút ngày 18 tháng 4 năm 2008. Dự án vệ tinh Vinasat-1 đã khởi hành từ năm 1998 với tổng mức đầu tư khoảng hơn 300 triệu USD. Việt Nam đã tiến hành đàm phán với 27 quốc gia và vùng lãnh thổ để có được vị trí 132 độ Đông trên quỹ đạo địa tĩnh.
Hãy tìm khoảng cách từ vị trí Vinasat-1 (vị trí A ) đến mặt đất (vị trí điểm H ). Biết rằng khi vệ tinh phát ra tín hiệu vô tuyến đến một điểm xa nhất trên mặt đất (vị trí M) thì từ lúc phát tín hiệu đến mặt đất cho đến lúc vệ tinh thu lại được tín hiệu phản hồi mất khoảng thời gian 0,28 giây. Trái Đất được xem như một hình cầu có bán kính khoảng 6400 km . Giả sử vận tốc sóng vô tuyến là \(3 \cdot {10^8}\;{\rm{m}}/{\rm{s}}\).
Câu hỏi trong đề: 62 bài tập Đa giác nội tiếp và đa giác đều có lời giải !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Độ dài AM là \(0,14 \cdot 3 \cdot {10^8} = 0,42 \cdot {10^8}(\;{\rm{m}}) = 0,42 \cdot {10^5}(\;{\rm{km}})\).
Xét vuông tại M , ta có: \({\rm{O}}{{\rm{A}}^2} = {\rm{A}}{{\rm{M}}^2} + {\rm{O}}{{\rm{M}}^2}\) (định lý Pythagore).\( \Rightarrow {\rm{OA}} = \sqrt {{\rm{A}}{{\rm{M}}^2} + {\rm{O}}{{\rm{M}}^2}} \)
Ta có: \({\rm{AH}} = {\rm{OA}} - {\rm{OH}} = \sqrt {{\rm{A}}{{\rm{M}}^2} + {\rm{O}}{{\rm{M}}^2}} - {\rm{OH}} = \sqrt {{{\left( {0,42 \cdot {{10}^5}} \right)}^2} + {{6400}^2}} - 6400 \approx 36085(\;{\rm{km}})\).
Vậy khoảng cách từ vị trí Vinasat-1 (vị trí A) đến mặt đất (vị trí điểm H) khoảng 36085 km .
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
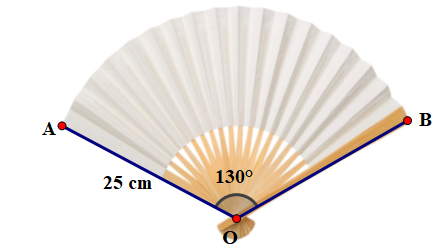
a) Diện tích hình quạt là: \({\rm{S}} = \frac{{\pi {{\rm{R}}^2}{\rm{n}}}}{{360}} = \frac{{\pi \cdot {{25}^2} \cdot 130}}{{360}} \approx 709\left( {\;{\rm{c}}{{\rm{m}}^2}} \right)\).
b) Diện tích giấy làm 100 cây quạt là: \(709 \cdot 2 \cdot 100 = 141800\left( {\;{\rm{c}}{{\rm{m}}^2}} \right)\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
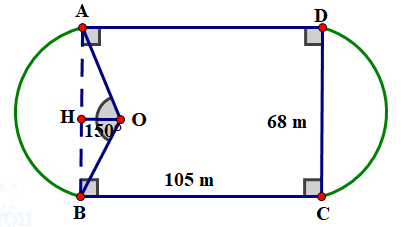
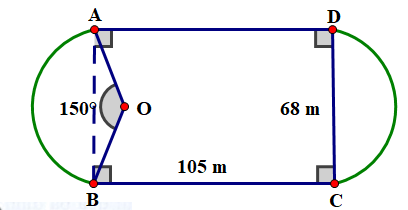
Kẻ \({\rm{OH}} \bot {\rm{AB}}\) tại \(H\), ta có:
Xét vuông tại \(H\), ta có:
Độ dài cung AB là:
Vậy chu vi sân khoảng 394,3 m.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập