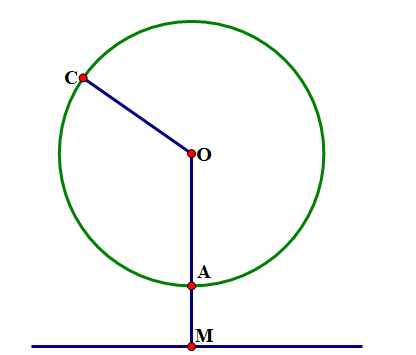
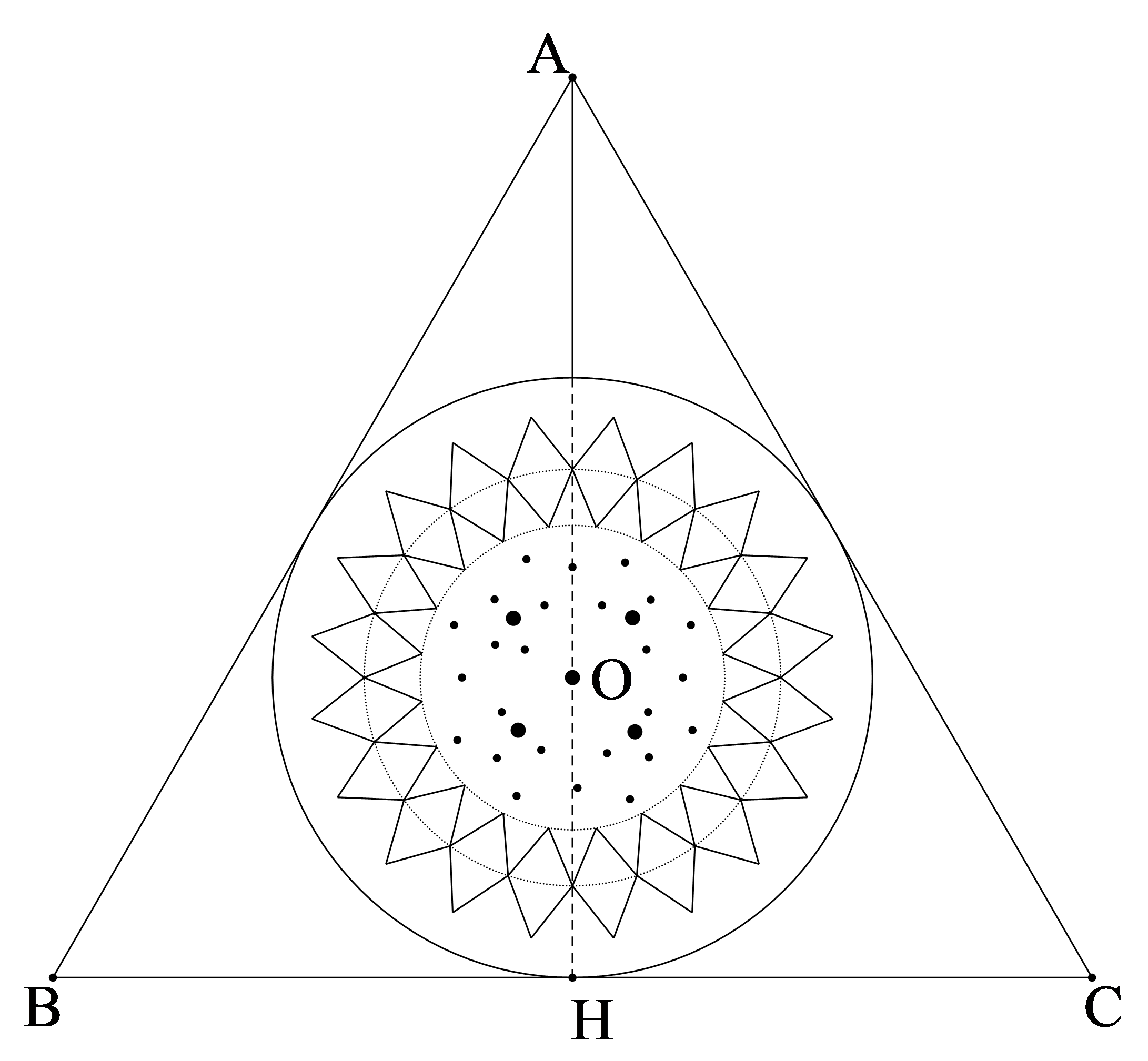Ngọn Hải đăng Kê Gà ở tỉnh Bình Thuận là ngọn tháp thắp đèn gần bờ biển dùng để định hướng cho tàu thuyền giao thông trong khu vực vào ban đêm. Đây là ngọn Hải đăng được xem là cổ xưa và cao nhất Việt Nam, chiều cao của ngọn đèn so với mặt nước biển là \(65m\) . Hỏi:
a) Một người quan sát đứng tại vị trí đèn của Hải đăng nhìn xa tối đa bao nhiêu km trên mặt biển?
b) Cách bao xa thì một người quan sát đứng ở trên tàu bắt đầu trông thấy ngọn đèn này, biết rằng mắt người quan sát đứng ở trên tàu có độ cao \(5m\) so với mặt nước biển?
(Cho biết bán kính Trái Đất gần bằng \(6400km\) và điều kiện quan sát trên biển là không bị che khuất).
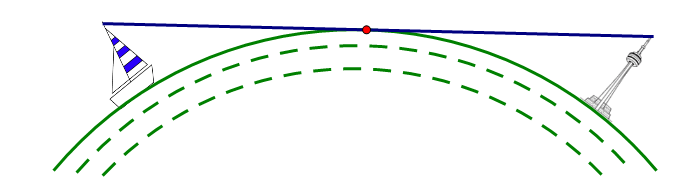
a) Một người quan sát đứng tại vị trí đèn của Hải đăng nhìn xa tối đa bao nhiêu km trên mặt biển?
b) Cách bao xa thì một người quan sát đứng ở trên tàu bắt đầu trông thấy ngọn đèn này, biết rằng mắt người quan sát đứng ở trên tàu có độ cao \(5m\) so với mặt nước biển?
(Cho biết bán kính Trái Đất gần bằng \(6400km\) và điều kiện quan sát trên biển là không bị che khuất).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Lời giải
\(65\;{\rm{m}} = 0,065\;{\rm{km}};5\;{\rm{m}} = 0,005\;{\rm{km}}\)
a) Ta có đồng dạng nên\(\frac{{MT}}{{MB}} = \frac{{MA}}{{MT}} \Rightarrow {M^2} = MA \cdot MB\)
\(MT = \sqrt {MA \cdot MB} = \sqrt {0,065 \cdot (0,065 + 2 \cdot 6400)} \approx 29(\;{\rm{km}})\)
Vậy một người quan sát đứng tại vị trí đèn của hải đăng nhìn xa tối đa khoảng 29 km .
b) Tương tự ta tính được: \({\rm{NT}} = \sqrt {{\rm{N}}{{\rm{O}}^2} - {\rm{O}}{{\rm{T}}^2}} = \sqrt {{{(0,005 + 6400)}^2} - {{6400}^2}} \approx 8(\;{\rm{km}})\).
Suy ra \({\rm{MN}} = 29 + 8 = 37(\;{\rm{km}})\).
Vậy cách khoảng 37 km thì một người quan sát đứng ở trên tàu bắt đầu trông thấy ngọn đèn này.
\(65\;{\rm{m}} = 0,065\;{\rm{km}};5\;{\rm{m}} = 0,005\;{\rm{km}}\)
a) Ta có đồng dạng nên\(\frac{{MT}}{{MB}} = \frac{{MA}}{{MT}} \Rightarrow {M^2} = MA \cdot MB\)
\(MT = \sqrt {MA \cdot MB} = \sqrt {0,065 \cdot (0,065 + 2 \cdot 6400)} \approx 29(\;{\rm{km}})\)
Vậy một người quan sát đứng tại vị trí đèn của hải đăng nhìn xa tối đa khoảng 29 km .
b) Tương tự ta tính được: \({\rm{NT}} = \sqrt {{\rm{N}}{{\rm{O}}^2} - {\rm{O}}{{\rm{T}}^2}} = \sqrt {{{(0,005 + 6400)}^2} - {{6400}^2}} \approx 8(\;{\rm{km}})\).
Suy ra \({\rm{MN}} = 29 + 8 = 37(\;{\rm{km}})\).
Vậy cách khoảng 37 km thì một người quan sát đứng ở trên tàu bắt đầu trông thấy ngọn đèn này.
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
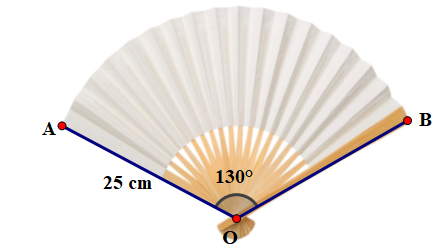
a) Diện tích hình quạt là: \({\rm{S}} = \frac{{\pi {{\rm{R}}^2}{\rm{n}}}}{{360}} = \frac{{\pi \cdot {{25}^2} \cdot 130}}{{360}} \approx 709\left( {\;{\rm{c}}{{\rm{m}}^2}} \right)\).
b) Diện tích giấy làm 100 cây quạt là: \(709 \cdot 2 \cdot 100 = 141800\left( {\;{\rm{c}}{{\rm{m}}^2}} \right)\).
Lời giải
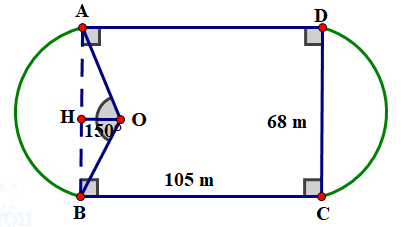
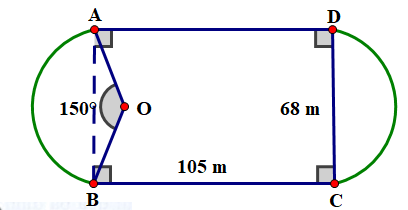
Kẻ \({\rm{OH}} \bot {\rm{AB}}\) tại \(H\), ta có:
Xét vuông tại \(H\), ta có:
Độ dài cung AB là:
Vậy chu vi sân khoảng 394,3 m.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
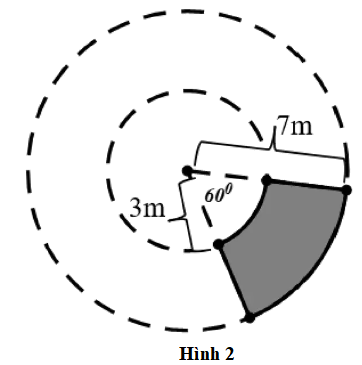
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập