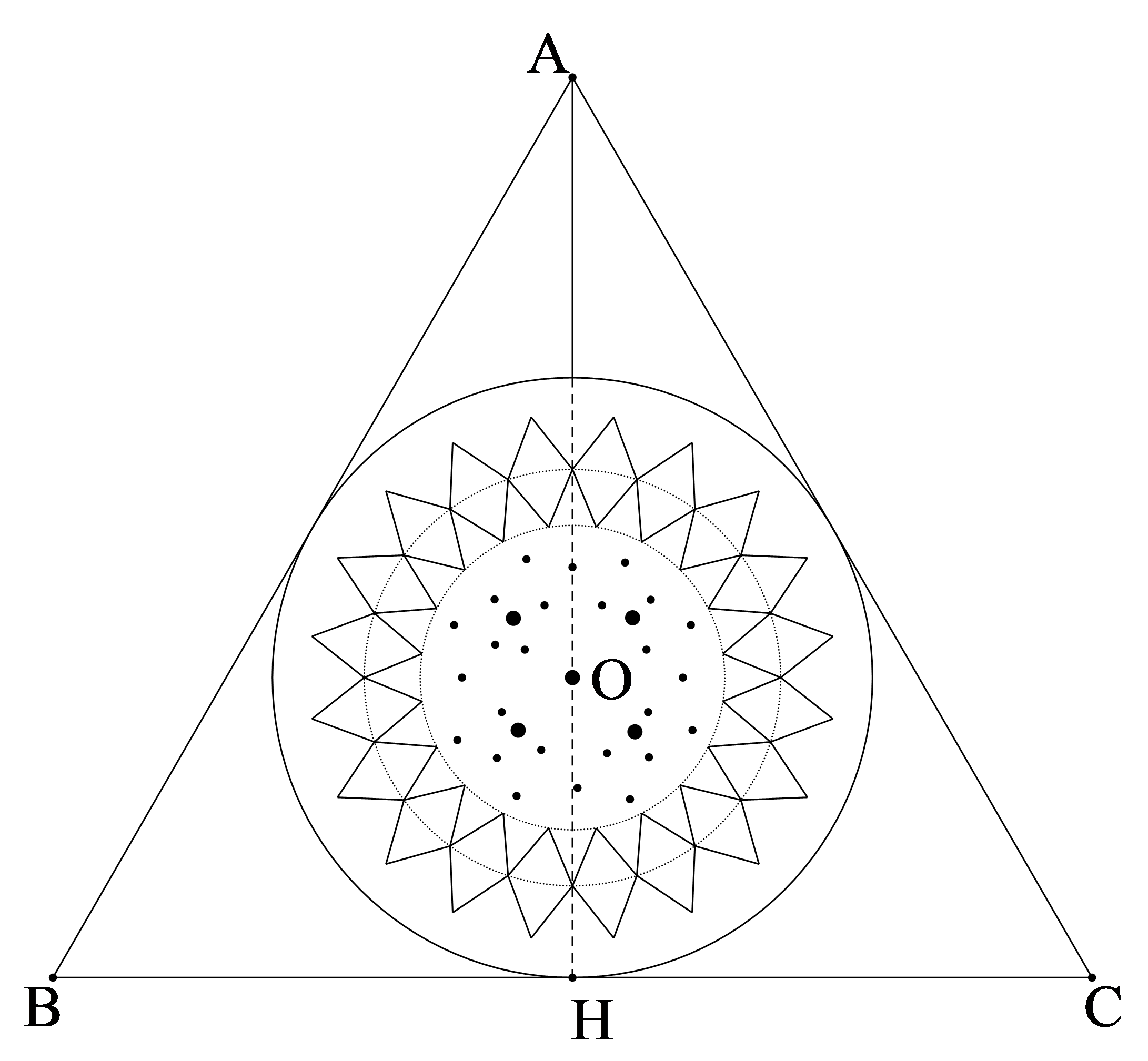khoahoc.vietjack.com
Giảm 50% Kích hoạt VIP
khoahoc.vietjack.com
Kích hoạt VIP Đăng nhập
Tạo VIP
  2. Ôn vào 10
  3. Toán

Câu hỏi:

13/04/2025 822 Lưu

Người ta muốn phục chế lại một đĩa cổ hình tròn bị vỡ chỉ còn lại một mảnh. Làm thế nào để xác định được bán kính của đĩa cổ này.

Xem lời giải

Câu hỏi trong đề: 62 bài tập Đa giác nội tiếp và đa giác đều có lời giải !!

Flashcard Bắt Đầu Thi Giao bài

Quảng cáo

Trả lời:

verified Giải bởi Vietjack

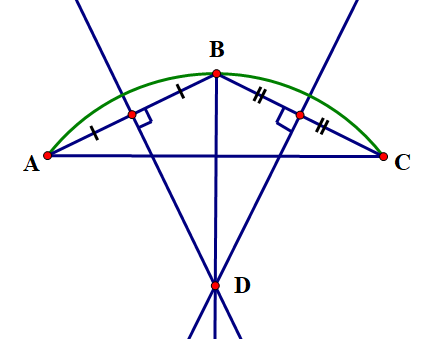
Người ta muốn phục chế lại một đĩa cổ hình tròn bị vỡ chỉ còn lại một mảnh. Làm thế nào để xác định được bán kính của đĩa cổ này. (ảnh 1)

Để xác định được bán kính ta cần xác định được tâm của đường tròn chứa chi tiết máy này. Ta xác định tâm như sau:

- Lấy ba điểm phân biệt \(A,B,C\) trên đường viền ngoài chiếc đĩa.

- Vẽ đường trung trực cạnh \(AB\)và cạnh \(BC\). Hai đường trung trực này cắt nhau tại \(D\). Khi đó\(D\)là tâm cần xác định.

- Bán kính đường tròn cần tìm là độ dài đoạn \(DB\) (hoặc \(DA\) hoặc \(DC\)).

Đang tải chế độ Học...

Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay

ĐẶC QUYỀN VIP

Đăng ký VIP để học và luyện thi không giới hạn

Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.

  • Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
  • Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
  • Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
  • Tải xuống đề thi [DOCX] với đầy đủ đáp án
  • Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
  • Bao gồm tất cả các bậc từ Tiểu học đến Đại học
  • Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
  • Đăng ký ngay
Avatar

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Một cây quạt giấy có bán kính 25 cm , biết AOB^=130° (hình vẽ bên).
a) Em hãy tính diện tích hình quạt AOB được tạo bởi cây quạt giấy? (kết quả làm tròn đến hàng đơn vị).
b) Tính diện tích giấy để làm 100 cây quạt. Biết quạt dán 2 mặt và phần mép dán không đáng kể.
Em hãy tính diện tích hình quạt AOB được tạo bởi cây quạt giấy? (kết quả làm tròn đến hàng đơn vị). (ảnh 1)

Lời giải

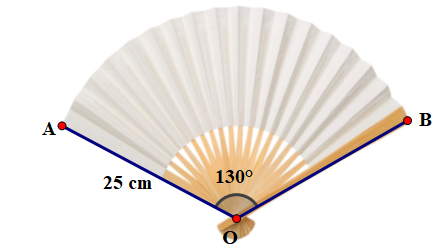
a) Diện tích hình quạt là: \({\rm{S}} = \frac{{\pi {{\rm{R}}^2}{\rm{n}}}}{{360}} = \frac{{\pi \cdot {{25}^2} \cdot 130}}{{360}} \approx 709\left( {\;{\rm{c}}{{\rm{m}}^2}} \right)\).

b) Diện tích giấy làm 100 cây quạt là: \(709 \cdot 2 \cdot 100 = 141800\left( {\;{\rm{c}}{{\rm{m}}^2}} \right)\).

Câu 2

Một sân vận động có hình dạng và kích thước được mô phỏng như hình vẽ. Biết BC=105 m,DC=68 m,AOB^=150°. Hãy tính chu vi của sân vận động trên? (Làm tròn đến hàng phần trăm).

Hãy tính chu vi của sân vận động trên? (ảnh 1)

Lời giải

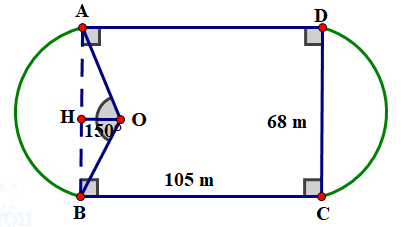
Hãy tính chu vi của sân vận động trên? (ảnh 2)

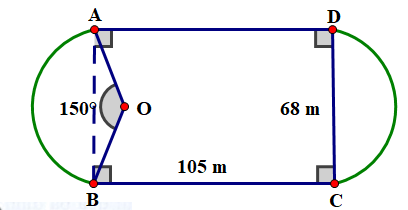
Kẻ \({\rm{OH}} \bot {\rm{AB}}\) tại \(H\), ta có: AOH=12AOB=12⋅150°=75° và AH=AB2=682=34( m)

Xét △AOH vuông tại \(H\), ta có: sinAOH=AHOA⇒OA=AHsinAOH=34sin75°(m)

Độ dài cung AB là: lAB=πRn180=π⋅34sin75°⋅150180≈92,15( m)

Vậy chu vi sân khoảng 394,3 m.

Câu 3

Tại một vòng xoay ngã tư, người ta cần làm các bồn trồng hoa như hình 1 . Em hãy tính phần diện tích của 1 bồn hoa ở hình 2 (phần được tô đậm). Biết rằng bán kính của vòng tròn lớn là 7 m , vòng tròn nhỏ là 3 m và góc ở tâm là 600

Em hãy tính phần diện tích của 1 bồn hoa ở hình 2 (ảnh 1)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Đài phun nước ở Công viên Hồ Khánh Hội, TP HCM vừa khánh thành vào ngày 31/08/2019. Đài phun nước có dạng đường tròn (gọi là đường tròn tâm \[O\]) và được thiết kế theo hình dáng những cánh hoa đan xen nhau, bên dưới là hệ thống phun nước với nhiều độ cao khác nhau kết hợp với hệ thống chiếu sáng và âm nhạc cùng các mảng cây xanh tạo không gian đô thị vui tươi, sinh động.  Một học sinh vẽ tam giác đều \[ABC\] ngoại tiếp đường tròn\[\left( O \right)\]và tính được diện tích tam giác đều là \[1\,200\]m2. Bạn hãy tính bán kính và chu vi của đường tròn \[\left( O \right)\]. (Kết quả làm tròn một chữ số thập phân và p = 3,14).

Bạn hãy tính bán kính và chu vi của đường tròn (ảnh 1)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Dùng \(1\) mảnh vải hình tròn để phủ lên \(1\) chiếc bàn tròn có diện tích \(1849\pi \,\left( {{\rm{c}}{{\rm{m}}^{\rm{2}}}} \right)\), sao cho khăn rủ xuống khỏi mép bàn \(20\,{\rm{cm}}\)(không tính phần viền mép khăn). Tính diện tích phần khăn rủ xuống khỏi mép bàn?

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Một chiếc đu quay hình tròn có chu vi \(470\;{\rm{m}}\) , tâm của vòng quay ở độ cao \(80\;{\rm{m}}\) so với mặt đất. Thời gian thực hiện mỗi vòng đu quay là 30 phút.

a) Tính bán kính của đu quay (làm tròn đến hàng đơn vị).

b) Nếu một người vào cabin ở vị trí thấp nhất của đu quay thì sau 10 phút người đó có độ cao bao nhiêu so với mặt đất (giả sử đu quay quay đều trong suốt quá trình quay).

Tính bán kính của đu quay (làm tròn đến hàng đơn vị). (ảnh 1)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 7

Trong 20 giây bánh xe của xe gắn máy quay được 60 vòng. Tính độ dài quãng đường xe gắn máy đã đi được trong vòng 3 phút, biết rằng bán kính bánh xe gắn máy bằng \(22\;{\rm{cm}}\) . (kết quả làm tròn đến hàng đơn vị, đơn vị là mét).

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Đăng ký

Bạn đã có tài khoản?

Khóa học 1 - 12
THPT
THCS
Phòng luyện đề
ĐGNL - ĐGTD
Tốt nghiệp THPT
Ôn vào 10
Ôn vào 6
Tài liệu
THPT
THCS
Tin Tuyển Sinh
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
Giấy chứng nhận ĐKKD số: 0108307822 do Sở KH & ĐT TP Hà Nội cấp lần đầu ngày 04/06/2018
© 2017 Vietjack37. All Rights Reserved.
zalo Nhắn tin Zalo Hỏi bài tập