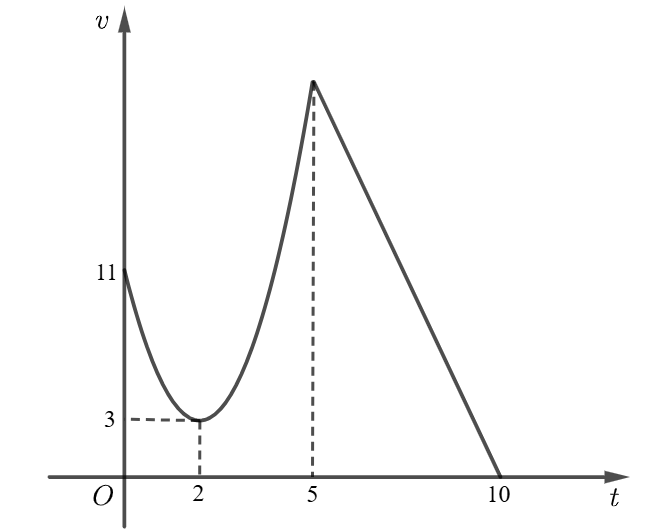
Một chất điểm chuyển động theo quy luật với tốc độ \[v\left( t \right)\,\,{\rm{(m/s)}}\], biết rằng \[v\left( t \right)\] có dạng đường parabol \[\left( P \right)\] đỉnh \[I\left( {2;3} \right)\] khi \[0 \le t \le 5\,\,{\rm{(s)}}\] và \[v\left( t \right)\] có dạng đường thẳng khi \[5 \le t \le 10\,\,{\rm{(s)}}\] như hình vẽ dưới đây.
a) Phương trình parabol \[\left( P \right)\] là \[v\left( t \right) = 2{t^2} - 8t + 10\].
Một chất điểm chuyển động theo quy luật với tốc độ \[v\left( t \right)\,\,{\rm{(m/s)}}\], biết rằng \[v\left( t \right)\] có dạng đường parabol \[\left( P \right)\] đỉnh \[I\left( {2;3} \right)\] khi \[0 \le t \le 5\,\,{\rm{(s)}}\] và \[v\left( t \right)\] có dạng đường thẳng khi \[5 \le t \le 10\,\,{\rm{(s)}}\] như hình vẽ dưới đây.

a) Phương trình parabol \[\left( P \right)\] là \[v\left( t \right) = 2{t^2} - 8t + 10\].
Quảng cáo
Trả lời:
a) Sai.
+) Parabol \(\left( P \right)\) có đỉnh \(I\left( {2;3} \right)\) nên phương trình \(\left( P \right)\) có dạng: \(v = a{\left( {t - 2} \right)^2} + 3\).
+) \(\left( P \right)\) đi qua điểm có tọa độ \(\left( {0;11} \right)\) nên \(11 = 4a + 3 \Leftrightarrow a = 2\).
Vậy phương trình \(\left( P \right)\) là \(v = 2{\left( {t - 2} \right)^2} + 3\) hay \[v\left( t \right) = 2{t^2} - 8t + 11\].
Theo đồ thị, khi \(t = 5 \Rightarrow v\left( 5 \right) = 21\).
+) Đường thẳng \(d\) có dạng: \(v = mt + n\).
+) Đường thẳng \(d\) đi qua hai điểm \(\left( {5;21} \right)\) và \(\left( {10;0} \right)\) nên \(\left\{ \begin{array}{l}5m + n = 21\\10m + n = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m = - \frac{{21}}{5}\\n = 42\end{array} \right.\).
Vậy phương trình \(d:v = - \frac{{21}}{5}t + 42\).
Do đó
Câu hỏi cùng đoạn
Câu 2:
b) Quãng đường vật di chuyển được trong khoảng thời gian từ \(0\)giây đến \(5\) giây là \[\frac{{115}}{3}\,\,{\rm{(m)}}\].
b) Quãng đường vật di chuyển được trong khoảng thời gian từ \(0\)giây đến \(5\) giây là \[\frac{{115}}{3}\,\,{\rm{(m)}}\].
b) Đúng. Quãng đường vật di chuyển được trong khoảng thời gian từ \(0\)giây đến \(5\) giây là \({S_1} = \int\limits_0^5 {\left( {2{t^2} - 8t + 11} \right){\rm{d}}t} = \frac{{115}}{3}\,\,{\rm{(m)}}\).
Câu 3:
c) Quãng đường vật di chuyển được trong khoảng thời gian từ giây thứ 5 đến giây thứ 10 là \[\frac{{385}}{2}\,\,{\rm{(m)}}\].
c) Quãng đường vật di chuyển được trong khoảng thời gian từ giây thứ 5 đến giây thứ 10 là \[\frac{{385}}{2}\,\,{\rm{(m)}}\].
c) Sai. Quãng đường vật di chuyển được trong khoảng thời gian từ giây thứ 5 đến giây thứ 10 là \({S_2} = \int\limits_5^{10} {\left( { - \frac{{21}}{5}t + 42} \right){\rm{d}}t} = 52,5\,\,{\rm{(m)}}\).
Câu 4:
d) Diện tích hình phẳng giới hạn bởi đồ thị hàm số \[v\left( t \right),\] trục \[Ot\], và hai đường thẳng \[t = 0,t = 10\] là \[\frac{{395}}{6}\] (đvdt).
d) Diện tích hình phẳng giới hạn bởi đồ thị hàm số \[v\left( t \right),\] trục \[Ot\], và hai đường thẳng \[t = 0,t = 10\] là \[\frac{{395}}{6}\] (đvdt).
d) Sai. Diện tích hình phẳng giới hạn bởi đồ thị hàm số \[v\left( t \right),\] trục \[Ot\], và hai đường thẳng \[t = 0,t = 10\] là \(S = \int\limits_0^5 {\left( {2{t^2} - 8t + 11} \right){\rm{d}}t} + \int\limits_5^{10} {\left( { - \frac{{21}}{5}t + 42} \right){\rm{d}}t} = \frac{{545}}{6}\)(đvdt).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án: \(6,4\).
Số tiền cả vốn và lãi ông An phải trả cho ngân hàng sau 1 năm là \(200\left( {1 + 8\% } \right) = 216\) (triệu đồng).
Số cổ phiếu ông An mua là: \(200\,000\,000:50\,000 = 4\,000\) (cổ phiếu).
Số tiền ông An bán cổ phiếu là \(4\,000 \cdot 55\,600 = 222\,400\,000\) (đồng) \( = 222,4\) (triệu đồng).
Số tiền còn lại của ông An là \(222,4 - 216 = 6,4\) (triệu đồng).
Lời giải
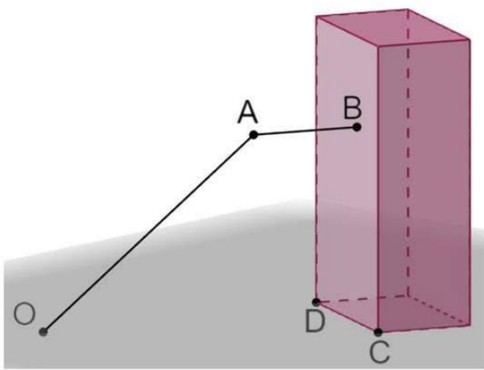
a) Đúng. Ta có \(OA = \sqrt {{{300}^2} + {{\left( { - 400} \right)}^2} + {{100}^2}} = \sqrt {260000} = 100\sqrt {26} \approx 509,9\, > 250\) nên radar không thể phát hiện UAV khi UAV ở vị trí \(A\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.