Cho hình chóp \[S.ABC\] có đáy \[ABC\] là tam giác đều cạnh \[a,\] cạnh bên \[SA\] vuông góc với mặt đáy, \(SA = \frac{{a\sqrt 6 }}{2}.\) Biết khoảng cách từ điểm \[A\] đến mặt phẳng \[\left( {SBC} \right)\] là \[ma\] (với \[m\] là số thực dương). Khi đó giá trị của \[m\] bằng bao nhiêu (làm tròn kết quả đến hàng phần trăm)?
Cho hình chóp \[S.ABC\] có đáy \[ABC\] là tam giác đều cạnh \[a,\] cạnh bên \[SA\] vuông góc với mặt đáy, \(SA = \frac{{a\sqrt 6 }}{2}.\) Biết khoảng cách từ điểm \[A\] đến mặt phẳng \[\left( {SBC} \right)\] là \[ma\] (với \[m\] là số thực dương). Khi đó giá trị của \[m\] bằng bao nhiêu (làm tròn kết quả đến hàng phần trăm)?
Quảng cáo
Trả lời:
Đáp án: 0,71.
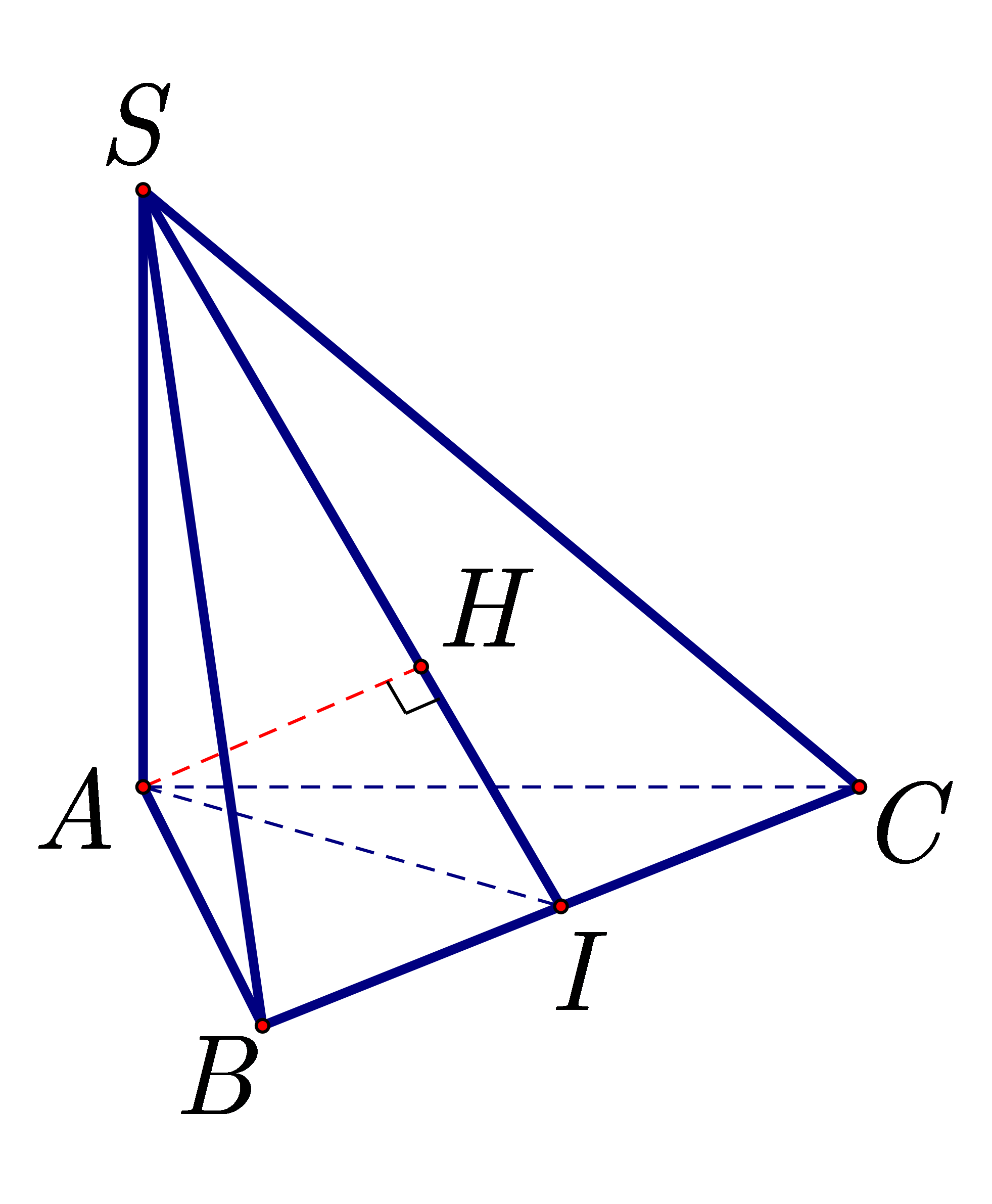
Gọi \(I\) là trung điểm của \(BC.\) Kẻ đường cao \(AH\) của tam giác \(SAC.\)
Ta có \(\Delta ABC\) đều nên \(BC \bot AI\). Mà \(SA \bot \left( {ABC} \right) \Rightarrow BC \bot SA\).
Suy ra \(BC \bot \left( {SAI} \right) \Rightarrow BC \bot AI.\)
Mặt khác \(AH \bot SI \subset \left( {SBC} \right) \Rightarrow AH \bot \left( {SBC} \right) \Rightarrow d\left( {A,\left( {SBC} \right)} \right) = AH\).
Xét tam giác vuông \(SAI\) có:
\(AI = \frac{{a\sqrt 3 }}{2},SA = \frac{{a\sqrt 6 }}{2} \Rightarrow A{H^2} = \frac{{A{I^2} \cdot S{A^2}}}{{A{I^2} + S{A^2}}} = \frac{{{a^2}}}{2} \Rightarrow AH = \frac{{\sqrt 2 }}{2}a \Rightarrow m \approx 0,71\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án: \(6,4\).
Số tiền cả vốn và lãi ông An phải trả cho ngân hàng sau 1 năm là \(200\left( {1 + 8\% } \right) = 216\) (triệu đồng).
Số cổ phiếu ông An mua là: \(200\,000\,000:50\,000 = 4\,000\) (cổ phiếu).
Số tiền ông An bán cổ phiếu là \(4\,000 \cdot 55\,600 = 222\,400\,000\) (đồng) \( = 222,4\) (triệu đồng).
Số tiền còn lại của ông An là \(222,4 - 216 = 6,4\) (triệu đồng).
Lời giải
a) Đúng. Ta có \(OA = \sqrt {{{300}^2} + {{\left( { - 400} \right)}^2} + {{100}^2}} = \sqrt {260000} = 100\sqrt {26} \approx 509,9\, > 250\) nên radar không thể phát hiện UAV khi UAV ở vị trí \(A\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.