Câu hỏi:
24/05/2025 258
Cho hình chóp \[S.ABCD\] có đáy là hình vuông cạnh \[2a,\,\,SA \bot \left( {ABCD} \right)\] và \[SA = 4a.\] Số đo góc nhị diện \[\left[ {B,SC,A} \right]\] bằng bao nhiêu độ (làm tròn kết quả đến hàng đơn vị)?
Cho hình chóp \[S.ABCD\] có đáy là hình vuông cạnh \[2a,\,\,SA \bot \left( {ABCD} \right)\] và \[SA = 4a.\] Số đo góc nhị diện \[\left[ {B,SC,A} \right]\] bằng bao nhiêu độ (làm tròn kết quả đến hàng đơn vị)?
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án: 51.
Cách 1:
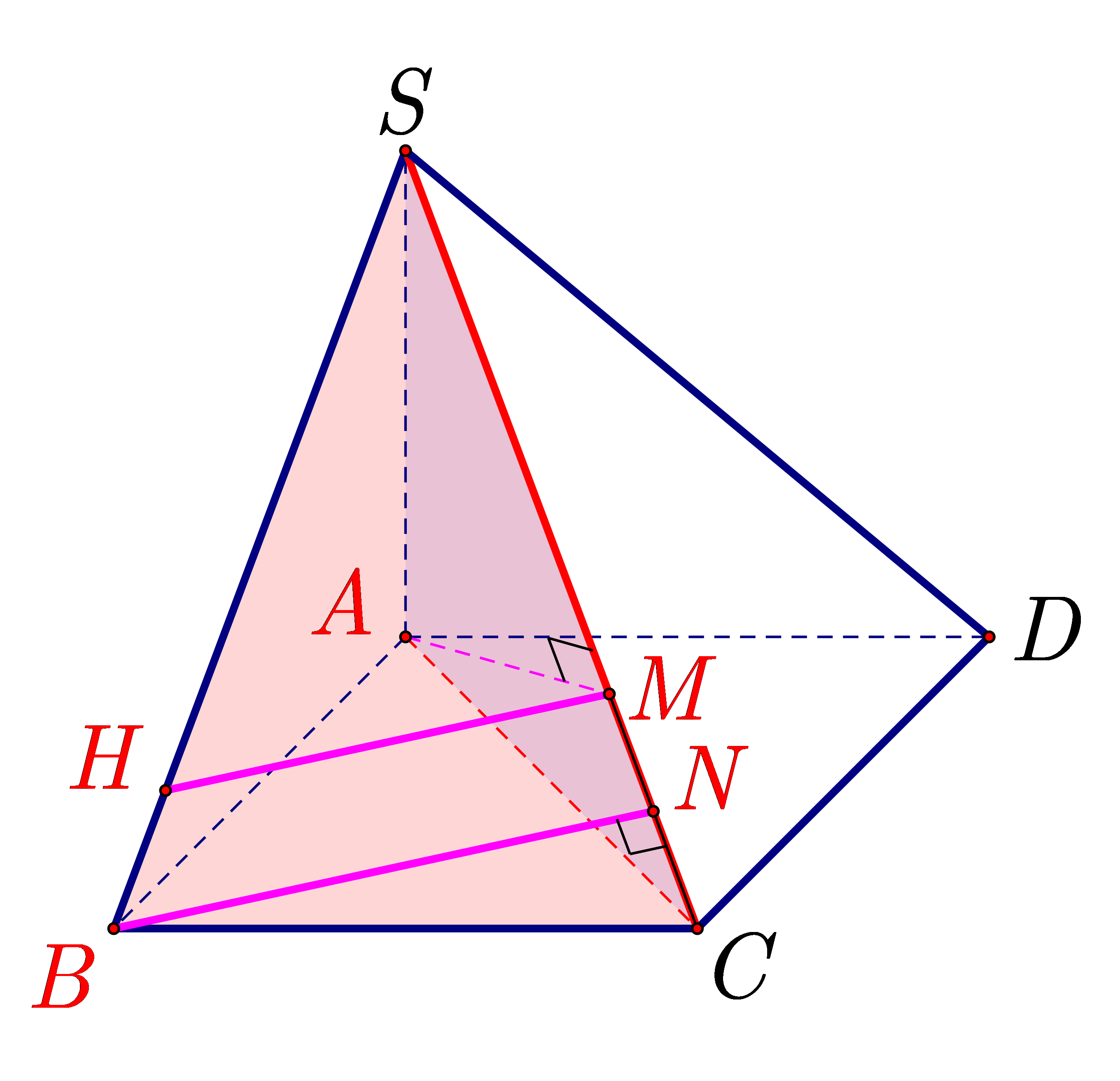
Ta có \(BC \bot AB,BC \bot SA\,\,\left( {SA \bot \left( {ABCD} \right)} \right) \Rightarrow BC \bot SB \Rightarrow \Delta SBC\) vuông tại \(B.\)
Ta xác định được \(SA = 4a,AB = 2a,AC = 2\sqrt 2 a,SC = 2\sqrt 6 a,SB = 2\sqrt 5 a.\)
Kẻ \(AM \bot SC\) tại \(M\). Xét tam giác vuông \(SAC\) có đường cao \(AM:\)
\(A{C^2} = SC \cdot CM \Leftrightarrow CM = \frac{{A{C^2}}}{{SC}} = \frac{{2a\sqrt 6 }}{3} = \frac{{SC}}{3}\);
\(AM = \frac{{SA \cdot AC}}{{SC}} = \frac{{4a \cdot 2a\sqrt 2 }}{{2a\sqrt 6 }} = \frac{{4\sqrt 3 }}{3}a\).
Kẻ \(BN \bot SC\) tại \(N\). Xét tam giác vuông \(SBC\) có đường cao \(BN:\)
\(B{C^2} = SC \cdot CN \Leftrightarrow CN = \frac{{B{C^2}}}{{SC}} = \frac{{a\sqrt 6 }}{3} = \frac{{SC}}{6};\,\,BN = \frac{{SB \cdot BC}}{{SC}} = \frac{{a\sqrt {30} }}{3}\).
Ta có \(\frac{{MH}}{{BN}} = \frac{{SM}}{{SN}} = \frac{{SC - \frac{{SC}}{3}}}{{SC - \frac{{SC}}{6}}} = \frac{4}{5} \Rightarrow MH = \frac{4}{5}BN = \frac{4}{5} \cdot \frac{{a\sqrt {30} }}{3} = \frac{{4a\sqrt {30} }}{{15}}\)(với .
Suy ra \(\left[ {B,SC,A} \right] = \widehat {AMH}\).
Xét tam giác \(SBN\) có: \(\frac{{SH}}{{SB}} = \frac{{SM}}{{SN}} \Leftrightarrow SH = \frac{{SM \cdot SB}}{{SN}} = \frac{4}{5} \cdot 2\sqrt 5 a = \frac{{8\sqrt 5 }}{5}a\).
Ta có \(A{H^2} = S{A^2} + S{H^2} - 2SA \cdot SH \cdot \cos \widehat {ASH} = S{A^2} + S{H^2} - 2 \cdot SA \cdot SH \cdot \frac{{SA}}{{SB}}\)
\( = 16{a^2} + \frac{{64}}{5}{a^2} - 2 \cdot 4a \cdot \frac{{8\sqrt 5 }}{5}a \cdot \frac{{4a}}{{2\sqrt 5 a}} = \frac{{16}}{5}{a^2}\).
\( \Rightarrow AH = \frac{{4\sqrt 5 }}{5}a\).
Khi đó, \(\cos \widehat {AMH} = \frac{{M{A^2} + M{H^2} - A{H^2}}}{{2MA.MH}} = \frac{{\frac{{16}}{3}{a^2} + \frac{{32}}{{15}}{a^2} - \frac{{16}}{5}{a^2}}}{{2 \cdot \frac{{4\sqrt 3 }}{3} \cdot a \cdot \frac{{4\sqrt {30} }}{{15}}a}} = \frac{{\sqrt {10} }}{5} \Rightarrow \widehat {AMH} \approx 51^\circ .\)
Cách 2:
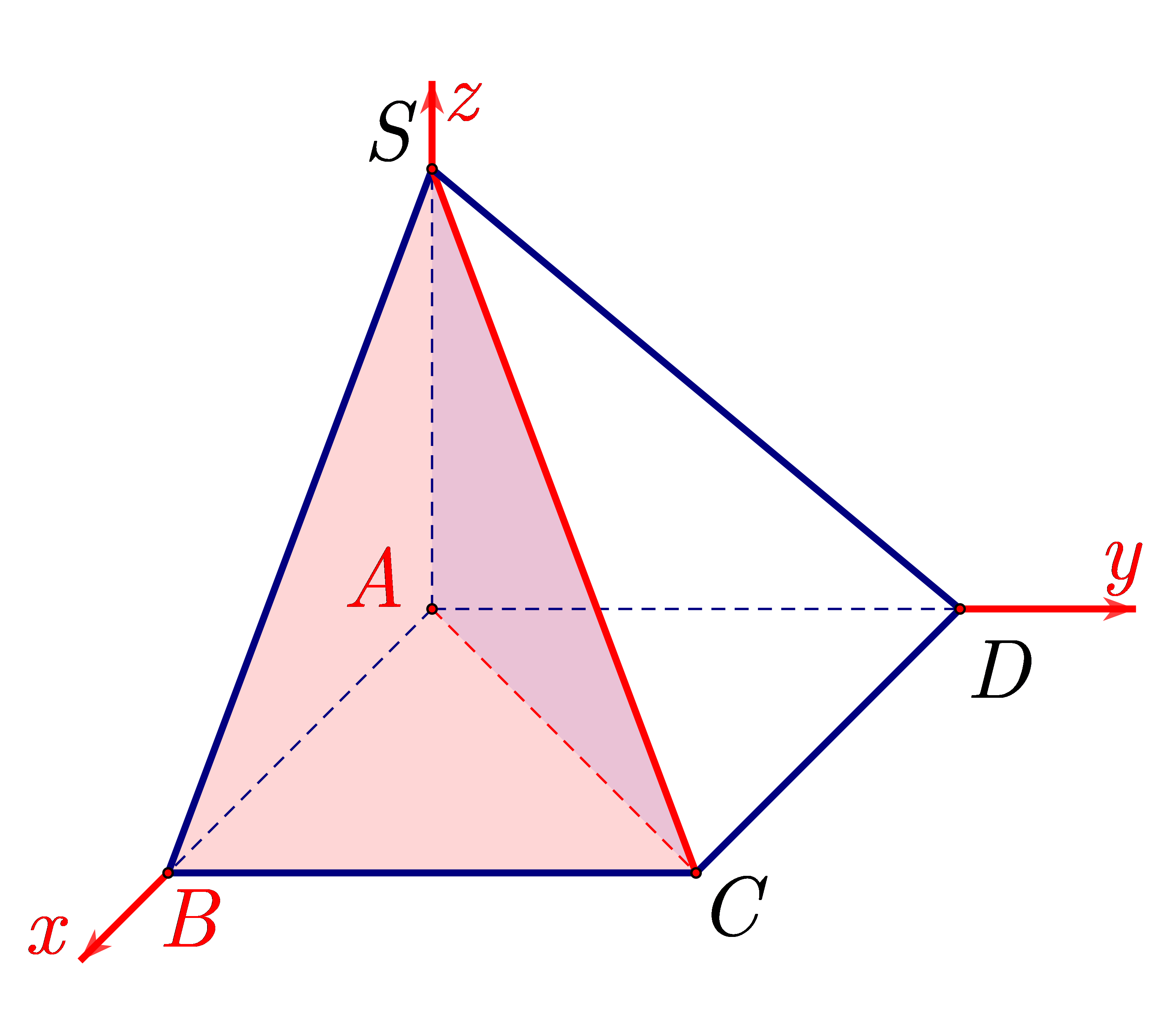
Chọn hệ trục tọa độ như hình vẽ trên thỏa mãn: \(O \equiv A\left( {0\,;0\,;0} \right),\,\,B \in Ox,\,\,D \in Oy,\,\,S \in Oz\).
Không mất tính tổng quát, ta suy ra được \(B\left( {2\,;0\,;0} \right),\,\,D\left( {0\,;2\,;0} \right),\,\,S\left( {0\,;0\,;4} \right){\rm{, }}C\left( {2\,;2\,;0} \right)\).
Gọi \({\vec n_1},{\vec n_2}\) lần lượt là vectơ pháp tuyến của các mặt phẳng \(\left( {SAC} \right),\left( {SBC} \right)\). Khi đó:
\[\left. \begin{array}{l}{{\vec n}_1} = \left[ {\overrightarrow {AC} ,\overrightarrow {AS} } \right] = 8\left( {1\,; - 1\,;0} \right)\\{{\vec n}_2} = \left[ {\overrightarrow {BS} ,\overrightarrow {BC} } \right] = - 4\left( {2\,;0\,;1} \right)\end{array} \right\} \Rightarrow \left| {\cos \left( {{{\vec n}_1},{{\vec n}_2}} \right)} \right| = \frac{{\sqrt {10} }}{5}\].
Suy ra \(\left[ {B,SC,A} \right] \approx 51^\circ \).
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi \(t\) là thời gian tính từ lúc xe Taxi bắt đầu chuyển động (\(t \ge 0\), đơn vị giây).
Vận tốc của xe Taxi: \({v_T}\left( t \right) = - \frac{1}{{180}}{t^2} + \frac{{116}}{{135}}t\) (m/s).
Xe Cứu thương xuất phát sau 1 giây (\(t = 1\)) với gia tốc \(a\) và vận tốc ban đầu \(0\).
Gọi \(t' = t - 1\) là thời gian chuyển động của xe Cứu thương (\(t' \ge 0\)).
Vận tốc xe Cứu thương: \({v_A}\left( {t'} \right) = at'\).
Quãng đường xe Cứu thương: \({S_A}\left( {t'} \right) = \frac{1}{2}a{\left( {t'} \right)^2}\).
a) Sai. Quãng đường xe Taxi đi được đến khi nhập làn (\(t = 20\)\[{\rm{s}}\]):
\({S_T}\left( {20} \right) = \int\limits_0^{20} {{v_T}\left( t \right)\,{\rm{d}}t} = \int\limits_0^{20} {\left( { - \frac{1}{{180}}{t^2} + \frac{{116}}{{135}}t} \right){\rm{d}}t} \) \[ = \left. {\left( { - \frac{{{t^3}}}{{540}} + \frac{{58}}{{135}}{t^2}} \right)} \right|_0^{20} = - \frac{{{{20}^3}}}{{540}} + \frac{{58}}{{135}} \cdot {20^2} = \frac{{4240}}{{27}} \approx 157\,{\rm{(m)}}\].
Lời giải
Đáp án: 3390.
Chọn hệ trục tọa độ \(Oxy\) sao cho parabol \(f\left( x \right) = a{x^2} + bx + c\) cắt trục hoành tại các điểm \(\left( { - 4;0} \right)\), \(\left( {24;0} \right)\) và tọa độ đỉnh \(I\left( {10; - \frac{{17}}{2}} \right)\).
Ta có hệ phương trình \(\left\{ {\begin{array}{*{20}{c}}\begin{array}{l}16a - 4b + c = 0\\576a + 24b + c = 0\,\,\,\,\,\,\end{array}\\{100a + 10b + c = - \frac{{17}}{2}}\end{array}} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}a = \frac{{17}}{{392}}\\b = - \frac{{85}}{{98}}\\c = - \frac{{204}}{{49}}\end{array} \right.\).
Nên \(f\left( x \right) = \frac{{17}}{{392}}{x^2} - \frac{{85}}{{98}}x - \frac{{204}}{{49}}\).
Thể tích của quả bóng bầu dục là:
\(V = \pi \int\limits_{ - 4}^{24} {{{\left[ {f\left( x \right)} \right]}^2}{\rm{d}}x = \pi } \int\limits_{ - 4}^{24} {{{\left[ {\frac{{17}}{{392}}{x^2} - \frac{{85}}{{98}}x - \frac{{204}}{{49}}} \right]}^2}{\rm{d}}x = } \frac{{16184\pi }}{{15}}\)\( \approx 3390\) (\({\rm{c}}{{\rm{m}}^{\rm{3}}}\)).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
30 Đề thi thử thpt quốc gia môn Toán có lời giải chi tiết mới nhất (Đề số 1)
-
CÂU TRẮC NGHIỆM ĐÚNG SAI
-
(2025 mới) Đề thi ôn tập THPT môn Toán có đáp án (Đề số 1)
-
Đề minh họa tốt nghiệp THPT môn Toán có đáp án năm 2025 (Đề 1)
-
Đề minh họa tốt nghiệp THPT môn Toán có đáp án năm 2025 (Đề 2)
-
Đề minh họa tốt nghiệp THPT môn Toán có đáp án năm 2025 (Đề 19)
-
(2025 mới) Đề thi ôn tập THPT môn Toán có đáp án (Đề số 2)
-
45 bài tập Xác suất có lời giải