Gọi A và B là hai giao điểm của đường thẳng y = x – 2 và parabol y = –x2. Độ dài đoạn thẳng AB là
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án đúng là: C
– Giả sử A(xA; yA) và B(xB; yB). Ta cần tính khoảng cách giữa hai điểm A và B là độ dài đoạn thẳng AB.
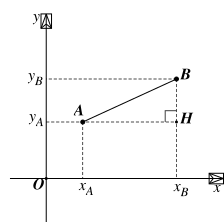
Qua A, B lần lượt kẻ đường thẳng song song với Ox, Oy. Hai đường thẳng này cắt nhau tại H. Khi đó tam giác ABH vuông tại H.
⦁ AH // Ox nên AH = |xA – xH| = |xA – xB|.
⦁ BH // Oy nên BH = |yA – yH| = |yA – yB|.
⦁ \(AB = \sqrt {A{H^2} + B{H^2}} = \sqrt {{{\left( {{x_A} - {x_B}} \right)}^2} + {{\left( {{y_A} - {y_B}} \right)}^2}} \) (Áp dụng định lí Pythagore cho ∆ABH vuông tại H).
– Gọi (x; y) là tọa độ giao điểm của đường thẳng (d): y = x – 2 và parabol (P): y = –x2, khi đó ta có:
y = –x2 (1) và y = x – 2.
Suy ra –x2 = x – 2 hay x2 + x – 2 = 0 (*).
Phương trình (*) có ∆ = 12 – 4.1.(–2) = 9 > 0 và \(\sqrt \Delta = \sqrt 9 = 3.\)
Do đó phương trình (*) có hai nghiệm phân biệt là:
\({x_1} = \frac{{ - 1 - 3}}{{2 \cdot 1}} = - 2;\,\,{x_2} = \frac{{ - 1 + 3}}{{2 \cdot 1}} = 1.\)
Với x1 = –2, thay vào (1), ta được: y = –(–2)2 = –4.
Với x2 = 1, thay vào (2), ta được: y = –12 = –1.
Như vậy, đường thẳng (d) cắt (P) tại hai điểm phân biệt có tọa độ là (–2; –4) và (1; –1).
Vậy độ dài đoạn thẳng AB là:
\[AB = \sqrt {{{\left( { - 2 - 1} \right)}^2} + {{\left[ { - 4 - \left( { - 1} \right)} \right]}^2}} = \sqrt {18} = 3\sqrt 2 .\]
Hot: 1000+ Đề thi cuối kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Nhắn tin Zalo
Hỏi bài tập