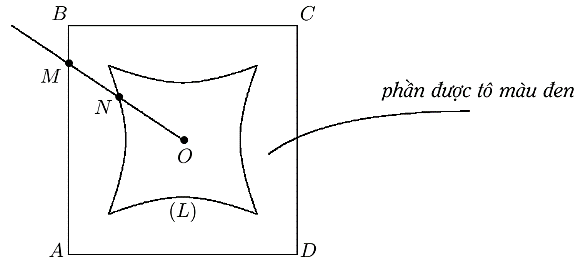
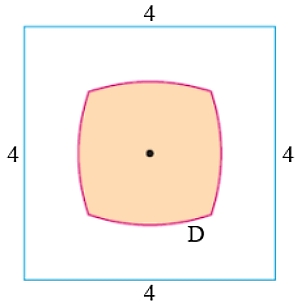
Trong một trò chơi điện tử, hai bạn Tít và Mít thi xem ai chạy được quãng đường xa hơn. Tít chạy với vận tốc \[{v_T}\,\left( t \right) = 5\sqrt t \] \[\left( {{\rm{km/h}}} \right)\], quãng đường Mít chạy được cho bởi phương trình \[{s_M}\left( t \right) = 5t - \frac{5}{{2\pi }}\sin \,\left( {2\pi t} \right)\]\[\left( {{\rm{km}}} \right)\] (với \[t\] là thời gian tính theo giờ). Nếu cuộc đua kết thúc khi Tít hoặc Mít chạy được \[10{\kern 1pt} {\kern 1pt} \,{\rm{km}}\] đầu tiên thì khoảng cách giữa hai bạn là bao nhiêu kilômét (kết quả làm tròn đến hàng phần trăm).
Trong một trò chơi điện tử, hai bạn Tít và Mít thi xem ai chạy được quãng đường xa hơn. Tít chạy với vận tốc \[{v_T}\,\left( t \right) = 5\sqrt t \] \[\left( {{\rm{km/h}}} \right)\], quãng đường Mít chạy được cho bởi phương trình \[{s_M}\left( t \right) = 5t - \frac{5}{{2\pi }}\sin \,\left( {2\pi t} \right)\]\[\left( {{\rm{km}}} \right)\] (với \[t\] là thời gian tính theo giờ). Nếu cuộc đua kết thúc khi Tít hoặc Mít chạy được \[10{\kern 1pt} {\kern 1pt} \,{\rm{km}}\] đầu tiên thì khoảng cách giữa hai bạn là bao nhiêu kilômét (kết quả làm tròn đến hàng phần trăm).
Quảng cáo
Trả lời:
Quãng đường Tít chạy là: \[{s_T}\,\left( t \right) = \int {{v_T}\left( t \right){\rm{d}}t{\kern 1pt} } {\kern 1pt} = \,{\kern 1pt} \int {5\sqrt t \,{\rm{d}}t} = \frac{{10}}{3}{\sqrt t ^3} + c\].
Khi \[t = 0\] thì \[{s_T} = 0\, \Rightarrow {\kern 1pt} {\kern 1pt} c = 0\]. Do đó \[{s_T}\,\left( t \right) = \frac{{10}}{3}{\sqrt t ^3}\].
Tít chạy được quãng đường \[10{\kern 1pt} \,{\kern 1pt} {\rm{km}}\]: \[{s_T}\,\left( t \right) = \frac{{10}}{3}{\sqrt t ^3} = 10 \Rightarrow {t_T} = \sqrt[3]{9}\,\,\left( {\rm{h}} \right)\].
Mít chạy được quãng đường \[10{\kern 1pt} {\kern 1pt} \,{\rm{km}}\]: \[{s_M}\left( t \right) = 5t - \frac{5}{{2\pi }}\sin \,\left( {2\pi t} \right) = 10\].
Xét \[{s'_M}\left( t \right) = 5 - 5\cos \left( {2\pi t} \right) \ge 0\,\forall t\] mà \[{s_M}\left( 2 \right) = 10\], suy ra \[{t_M} = 2\,\,\left( {\rm{h}} \right)\].
Ta thấy \[{t_M} < {t_T}\] nên Mít chạy được \[10{\kern 1pt} {\kern 1pt} \,{\rm{km}}\] đầu tiên. Khi đó khoảng cách giữa hai bạn là
\[{s_M}\,\left( 2 \right) - {s_T}\,\left( 2 \right) = 10 - \frac{{10}}{3}{\sqrt 2 ^3} \approx 0,57\,\,\left( {{\rm{km}}} \right)\].
Đáp án: \[0,57\].
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
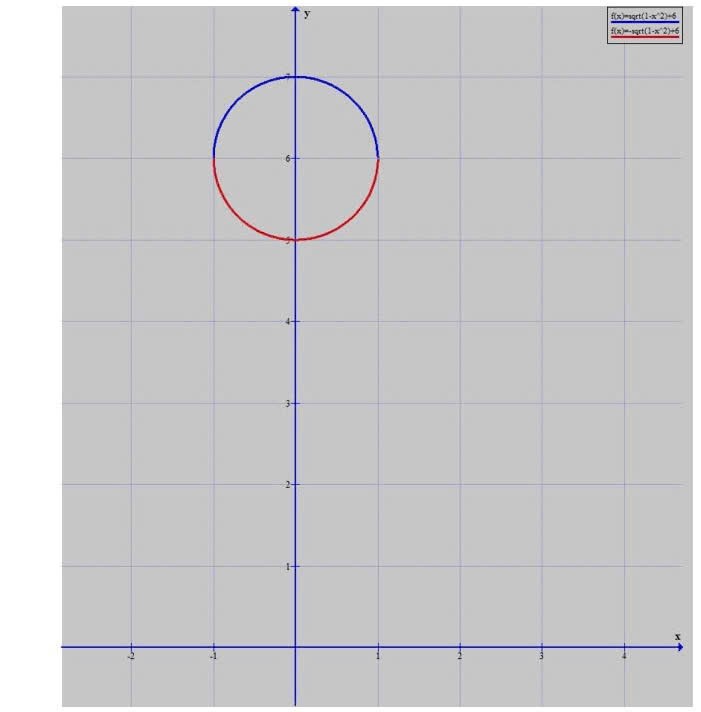
Gắn hệ trục tọa độ với gốc tọa độ là tâm của chiếc vòng, trục \(Ox\) là trục đối xứng của vòng, \(Oy\) đi qua tâm một thiết diện cắt ngang của vòng.
Khi đó phương trình đường tròn thiết diện là
\(\left( C \right):{x^2} + {\left( {y - 6} \right)^2} = 1 \Leftrightarrow y = 6 \pm \sqrt {1 - {x^2}} \).
Vòng được tạo ra bằng cách quay đường tròn \(\left( C \right):{x^2} + {\left( {y - 6} \right)^2} = 1\) quanh trục \(Ox\).
Thể tích của chiếc vòng là:
\[{V_{Ox}} = \pi \left[ {\int\limits_{ - 1}^1 {{{\left( {6 + \sqrt {1 - {x^2}} } \right)}^2}{\rm{d}}x - } \int\limits_{ - 1}^1 {{{\left( {6 - \sqrt {1 - {x^2}} } \right)}^2}{\rm{d}}x} } \right] = \pi \int\limits_{ - 1}^1 {24\sqrt {1 - {x^2}} } {\rm{d}}x = 12{\pi ^2} \approx 118\,\,\left( {{\rm{c}}{{\rm{m}}^{\rm{3}}}} \right)\].
Đáp án: \(118\).
Lời giải
Trong 24 giây chạy thử nghiệm đó, chiếc xe mô hình đi được quãng đường là:
\[s = \int\limits_0^{24} {v\left( t \right){\rm{d}}t} = \int\limits_0^8 {\frac{1}{2}t{\rm{d}}t + \int\limits_8^{16} {4{\rm{d}}t} + } \int\limits_{16}^{24} {\left( { - \frac{1}{2}t + 12} \right){\rm{d}}t} \,\;\, = \left. {\left( {\frac{1}{4}{t^2}} \right)} \right|_0^8 + \left. {\left( {4t} \right)} \right|_8^{16} + \left. {\left( { - \frac{1}{4}{t^2} + 12t} \right)} \right|_{16}^{24} = 64\,\,{\rm{(dm)}}\].
Đáp án: \[64\].
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Cho một chất điểm chuyển động theo quy luật vận tốc \[v\left( t \right)\]( đơn vị: \[{\rm{m/s}}\]) có đồ thị như hình vẽ bên. Trong đó đồ thị có dạng các đoạn thẳng tương ứng theo thời gian \[t\] giây khi \[0 \le t \le 3\], \[8 \le t \le 15\] và có dạng đường parabol tương ứng thời gian \[t\] giây khi \[3 \le t \le 8\].
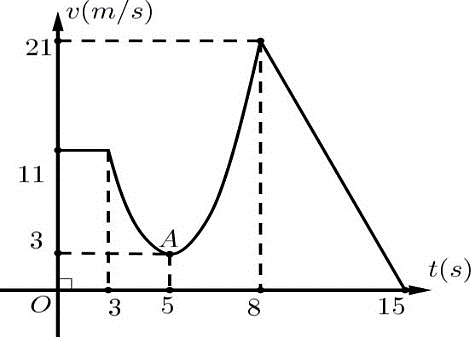
a) Vận tốc của chất điểm tại thời điểm \[t = 15\] là \[v\left( {15} \right) = 21\,\,\left( {{\rm{m/s}}} \right)\].
b) Quãng đường mà chất điểm đi được trong thời gian \[3\] giây đầu \[\left( {0 \le t \le 3} \right)\] là \(S = \int\limits_0^3 {11\,{\rm{d}}t\,\,\,{\rm{(m)}}} \).
c) Quãng đường mà chất điểm đi được trong khoảng thời gian \[7\] giây cuối \[\left( {8 \le t \le 15} \right)\] là \(73,5\,\,{\rm{m}}\).
d) Vận tốc trung bình \({v_{tb}}\) của chất điểm trong thời gian \[t\] giây \[\left( {3 \le t \le 8} \right)\] thỏa mãn \({v_{tb}} < 7\,\,\left( {{\rm{m/s}}} \right)\).

a) Vận tốc của chất điểm tại thời điểm \[t = 15\] là \[v\left( {15} \right) = 21\,\,\left( {{\rm{m/s}}} \right)\].
b) Quãng đường mà chất điểm đi được trong thời gian \[3\] giây đầu \[\left( {0 \le t \le 3} \right)\] là \(S = \int\limits_0^3 {11\,{\rm{d}}t\,\,\,{\rm{(m)}}} \).
c) Quãng đường mà chất điểm đi được trong khoảng thời gian \[7\] giây cuối \[\left( {8 \le t \le 15} \right)\] là \(73,5\,\,{\rm{m}}\).
d) Vận tốc trung bình \({v_{tb}}\) của chất điểm trong thời gian \[t\] giây \[\left( {3 \le t \le 8} \right)\] thỏa mãn \({v_{tb}} < 7\,\,\left( {{\rm{m/s}}} \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.