Khi chuyển động trong không gian, máy bay luôn chịu tác động của bốn lực chính: lực đẩy của động cơ, lực cản của không khí, trọng lực và lực nâng khí động học (H.2.20). Lực cản của không khí ngược hướng với lực đẩy của động cơ và có độ lớn tỉ lệ thuận với bình phương vận tốc máy bay. Một chiếc máy bay tăng vận tốc từ 900 km/h lên 920 km/h, trong quá trình tăng tốc máy bay giữ nguyên hướng bay. Lực cản của không khí khi máy bay đạt vận tốc 900 km/h và 920 km/h lần lượt được biểu diễn bởi hai vectơ \[\overrightarrow {{F_1}} \] và \[\overrightarrow {{F_2}} \]. Hãy giải thích vì sao \[\overrightarrow {{F_1}} = k\overrightarrow {{F_2}} \], với k là một số thực dương nào đó. Tính giá trị của k (làm tròn kết quả đến chữ số thập phân thứ hai).
Câu hỏi trong đề: Các dạng bài tập Vectơ trong không gian lớp 12 (có lời giải) !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Vì trong quá trình máy bay tăng vận tốc từ \(900\;{\rm{km}}/{\rm{h}}\) lên \(920\;{\rm{km}}/{\rm{h}}\) máy bay giữ nguyên hướng bay nên vectơ \({\vec F_1}\) và \({\vec F_2}\) có cùng hướng. Do đó, \({\vec F_1} = k{\vec F_2}\) với k là một số thực dương nào đó (1).
Gọi \({v_1},{v_2}\) lần lượt là vận tốc của của chiếc máy bay khi đạt \(900\;{\rm{km}}/{\rm{h}}\) và \(920\;{\rm{km}}/{\rm{h}}\).
Suy ra \({v_1} = 900(\;{\rm{km}}/{\rm{h}}),{v_2} = 920(\;{\rm{km}}/{\rm{h}})\)
vì lực cản của không khí ngược hướng với lực đẩy của động cơ và có độ lớn tỉ lệ thuận với bình phương vận tốc máy bay nên \(\frac{{\left| {{{\vec F}_1}} \right|}}{{\left| {{{\vec F}_2}} \right|}} = \frac{{v_1^2}}{{v_2^2}} = \frac{{{{900}^2}}}{{{{920}^2}}} = \frac{{2025}}{{2116}} \Rightarrow \left| {{{\vec F}_1}} \right| = \frac{{2025}}{{2116}}\left| {{{\vec F}_2}} \right|\)
Từ (1) và (2) ta có: \(\overrightarrow {{F_1}} = \frac{{2025}}{{2116}}\overrightarrow {{F_2}} \Rightarrow k = \frac{{2025}}{{2116}} \approx 0,96\)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
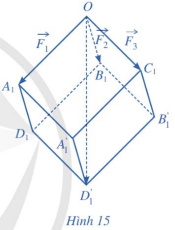
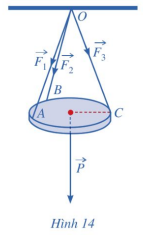
Gọi \[{A_1}{\rm{, }}{B_1},{C_1}\] lần lượt là các điểm sao cho \[\overrightarrow {O{A_1}} = \overrightarrow {{F_1}} ;\overrightarrow {O{B_1}} = \overrightarrow {{F_2}} ;\overrightarrow {O{C_1}} = \overrightarrow {{F_3}} \]. Lấy các điểm \[{D_1},{A'_1}{\rm{, }}{B'_1},{D'_1}\] sao cho \[O{A_1}{D_1}{B_1}.{C_1}{A'_1}{D'_1}B'\] là hình hộp (Hình 15).
Khi đó, áp dụng quy tắc hình hộp, ta có: \[{\overrightarrow {OA} _1} + \overrightarrow {O{B_1}} + \overrightarrow {O{C_1}} {\rm{ = }}\overrightarrow {O{D_1}} \]
Mặt khác, do các lực căng \[\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} ,\overrightarrow {{F_3}} \] đôi một vuông góc và \[\left| {\overrightarrow {{F_1}} } \right| = \left| {\overrightarrow {{F_2}} } \right| = \left| {\overrightarrow {{F_3}} } \right| = 15{\rm{ }}(N)\] nên hình hộp
\[O{A_1}{D_1}{B_1}.{C_1}{A'_1}{D'_1}B'\] có ba cạnh OA1, OB1, OC1, đôi một vuông góc và bằng nhau. Vì thế hình hộp đó là hình lập phương có độ dài cạnh bằng 15. Suy ra độ dài đường chéo \[O{D'_1}\] của hình lập phương đó bằng \[15\sqrt 3 \].
Do chiếc đèn ở vị trí cân bằng nên \[\overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} = \overrightarrow P \], ở đó \[\overrightarrow P \] là trọng lực tác dụng lên chiếc đèn. Suy ra trọng lượng của chiếc đèn là: \[\left| {\overrightarrow P } \right| = \left| {\overrightarrow {O{{D'}_1}} } \right| = 15\sqrt 3 \] (N).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập