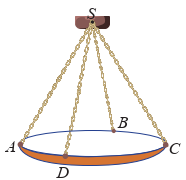
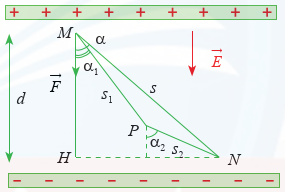
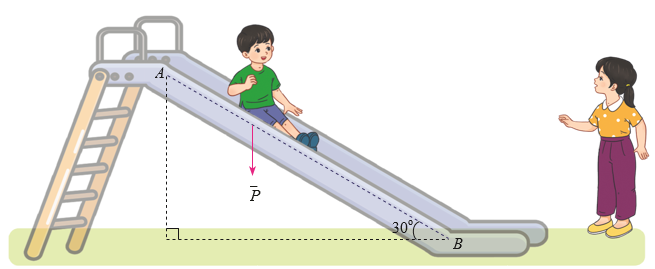
Ba sợi dây không giãn với khối lượng không đáng kể được buộc chung một đầu và được kéo căng về ba hướng khác nhau (H.2.31). Nếu các lực kéo làm cho ba sợi dây ở trạng thái đứng yên thì khi đó ba sợi dây nằm trên cùng một mặt phẳng. Hãy giải thích vì sao.


Quảng cáo
Trả lời:
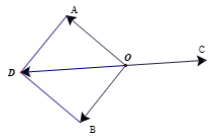
Giả sử lực kéo trên mỗi sợi dây được biếu diễn bởi các vectơ \(\overrightarrow {OA} ,\overrightarrow {OB} ,\overrightarrow {OC} \) với là đầu chung của ba sợi dây. Khi ba sợi dậy cân bằng thì \(\vec O + \overrightarrow {OB} + \overrightarrow {OC} = \vec 0\).
Vẽ hình bình hành \({\rm{OADB}}\).
Theo quy tắc hình bình hành thì \(\overrightarrow {OA} + \overrightarrow {OB} = \overrightarrow {OD} \).
Do đó \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = \vec 0 \Leftrightarrow \overrightarrow {OD} + \overrightarrow {OC} = \vec 0 \Leftrightarrow \overrightarrow {OC} = - \overrightarrow {OD} \).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Lời giải
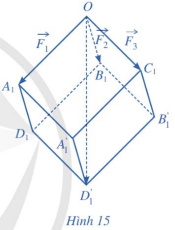
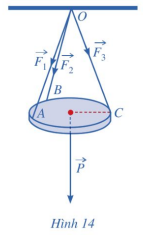
Gọi \[{A_1}{\rm{, }}{B_1},{C_1}\] lần lượt là các điểm sao cho \[\overrightarrow {O{A_1}} = \overrightarrow {{F_1}} ;\overrightarrow {O{B_1}} = \overrightarrow {{F_2}} ;\overrightarrow {O{C_1}} = \overrightarrow {{F_3}} \]. Lấy các điểm \[{D_1},{A'_1}{\rm{, }}{B'_1},{D'_1}\] sao cho \[O{A_1}{D_1}{B_1}.{C_1}{A'_1}{D'_1}B'\] là hình hộp (Hình 15).
Khi đó, áp dụng quy tắc hình hộp, ta có: \[{\overrightarrow {OA} _1} + \overrightarrow {O{B_1}} + \overrightarrow {O{C_1}} {\rm{ = }}\overrightarrow {O{D_1}} \]
Mặt khác, do các lực căng \[\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} ,\overrightarrow {{F_3}} \] đôi một vuông góc và \[\left| {\overrightarrow {{F_1}} } \right| = \left| {\overrightarrow {{F_2}} } \right| = \left| {\overrightarrow {{F_3}} } \right| = 15{\rm{ }}(N)\] nên hình hộp
\[O{A_1}{D_1}{B_1}.{C_1}{A'_1}{D'_1}B'\] có ba cạnh OA1, OB1, OC1, đôi một vuông góc và bằng nhau. Vì thế hình hộp đó là hình lập phương có độ dài cạnh bằng 15. Suy ra độ dài đường chéo \[O{D'_1}\] của hình lập phương đó bằng \[15\sqrt 3 \].
Do chiếc đèn ở vị trí cân bằng nên \[\overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} = \overrightarrow P \], ở đó \[\overrightarrow P \] là trọng lực tác dụng lên chiếc đèn. Suy ra trọng lượng của chiếc đèn là: \[\left| {\overrightarrow P } \right| = \left| {\overrightarrow {O{{D'}_1}} } \right| = 15\sqrt 3 \] (N).Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.