khoahoc.vietjack.com
Giảm 50% Kích hoạt VIP
khoahoc.vietjack.com
Kích hoạt VIP Đăng nhập
Tạo VIP
  2. Lớp 12
  3. Toán

Câu hỏi:

19/08/2025 991 Lưu

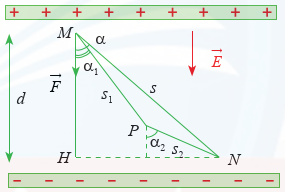
Ba lực có điểm đặt tại một đỉnh của hình lập phương, cùng phương với ba cạnh và cùng có cường độ là 5 N. Tính cường độ của hợp lực.

Xem lời giải

Câu hỏi trong đề: Các dạng bài tập Vectơ trong không gian lớp 12 (có lời giải) !!

Flashcard Bắt Đầu Thi Giao bài

Quảng cáo

Trả lời:

verified Giải bởi Vietjack
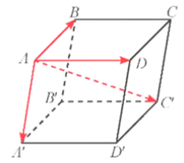
Ba lực có điểm đặt tại một đỉnh của hình lập phương, cùng phương với ba cạnh và cùng có cường độ là 5 N (ảnh 1)

Giả sử 3 lực có điếm đặt là \({\rm{A}}\) và các lực là \(\overrightarrow {AB} ,\overrightarrow {AD} ,\overrightarrow {A{A^\prime }} \).

Theo quy tắc hình bình hành ta có hợp lực: \(\overrightarrow {A{C^\prime }}  = \overrightarrow {AB}  + \overrightarrow {AD}  + \overrightarrow {A{A^\prime }} \). Theo đề ta có \(|\overrightarrow {AB} | = |\overrightarrow {AD} | = \left| {\overrightarrow {A{A^\prime }} } \right| = 5\).

Mà \({\rm{AC}}\) là đường chéo của của hình lập phương nên \(A{C^\prime } = \sqrt {A{B^2} + A{D^2} + A{A^{\prime 2}}}  = 5\sqrt 3 \) Vậy cường độ của hợp lực là \(5\sqrt 3 N\).

Đang tải chế độ Học...

Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay

ĐẶC QUYỀN VIP

Đăng ký VIP để học và luyện thi không giới hạn

Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.

  • Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
  • Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
  • Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
  • Tải xuống đề thi [DOCX] với đầy đủ đáp án
  • Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
  • Bao gồm tất cả các bậc từ Tiểu học đến Đại học
  • Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
  • Đăng ký ngay
Avatar

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho biết công A (đơn vị: J) sinh bởi lực \[\overrightarrow F \] tác dụng lên một vật được tính bằng công thức A = \[\overrightarrow F \]. \[\overrightarrow d \], trong đó \[\overrightarrow d \] là vectơ biểu thị độ dịch chuyển của vật (đơn vị của d là m) khi chịu tác dụng của lực \[\overrightarrow F \]. Một chiếc xe có khối lượng 1,5 tấn đang đi xuống trên một đoạn đường dốc có góc nghiêng 5° so với phương ngang. Tính công sinh bởi trọng lực \[\overrightarrow P \] khi xe đi hết đoạn đường dốc dài 30 m (làm tròn kết quả đến hàng đơn vị), biết rằng trọng lực \[\overrightarrow P \] được xác định bởi công thức \[\overrightarrow P \] = m\[\overrightarrow g \], với m (đơn vị: kg) là khối lượng của vật và \[\overrightarrow g \] là gia tốc rơi tự do có độ lớn g = 9,8 m/s2.

 

Lời giải

Ta có 1,5 tấn = 1 500 kg.
Độ lớn của trọng lực tác dụng lên chiếc xe là: \[\left| {\overrightarrow P } \right|\] = m \[\left| {\overrightarrow g } \right|\] = 1 500 . 9,8 = 14 700 (N). Vectơ \[\overrightarrow d \] biểu thị độ dịch chuyển của xe có độ dài là \[\left| {\overrightarrow d } \right|\] = 30 (m) và\[\left( {\overrightarrow P ,\overrightarrow d } \right) = {90^o} - {5^o} = {85^o}\]
 
Công sinh ra bởi trọng lực \[\overrightarrow P \] khi xe đi hết đoạn đường dốc dài 30 m là: A=P→.d→=P→.d→.cosP→,d→=14700.30.cos85o≈38436 (J)

Câu 2

Một chiếc đèn tròn được treo song song với mặt phẳng nằm ngang bởi ba sợi dây không dãn xuất phát từ điểm O trên trần nhà và lần lượt buộc vào ba điểm A, B, C trên đèn tròn sao cho các lực căng \[\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} ,\overrightarrow {{F_3}} \] lần lượt trên mỗi dây OA, OB, OC đôi một vuông góc với nhau và \[\left| {\overrightarrow {{F_1}} } \right| = \left| {\overrightarrow {{F_2}} } \right| = \left| {\overrightarrow {{F_3}} } \right| = 15{\rm{ }}(N)\]. (Hình 14). Tính trọng lượng của chiếc đèn tròn đó.
Media VietJack

Lời giải

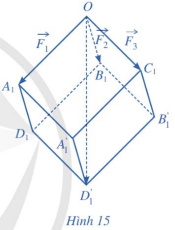
Một chiếc đèn tròn được treo song song với mặt phẳng nằm ngang bởi ba sợi dây không dãn xuất phát từ điểm O (ảnh 1)

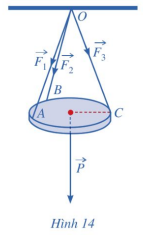
Gọi \[{A_1}{\rm{, }}{B_1},{C_1}\] lần lượt là các điểm sao cho \[\overrightarrow {O{A_1}}  = \overrightarrow {{F_1}} ;\overrightarrow {O{B_1}}  = \overrightarrow {{F_2}} ;\overrightarrow {O{C_1}}  = \overrightarrow {{F_3}} \]. Lấy các điểm \[{D_1},{A'_1}{\rm{, }}{B'_1},{D'_1}\] sao cho \[O{A_1}{D_1}{B_1}.{C_1}{A'_1}{D'_1}B'\] là hình hộp (Hình 15).  

Khi đó, áp dụng quy tắc hình hộp, ta có: \[{\overrightarrow {OA} _1} + \overrightarrow {O{B_1}}  + \overrightarrow {O{C_1}} {\rm{ = }}\overrightarrow {O{D_1}} \]

Mặt khác, do các lực căng \[\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} ,\overrightarrow {{F_3}} \] đôi một vuông góc và \[\left| {\overrightarrow {{F_1}} } \right| = \left| {\overrightarrow {{F_2}} } \right| = \left| {\overrightarrow {{F_3}} } \right| = 15{\rm{ }}(N)\] nên hình hộp

\[O{A_1}{D_1}{B_1}.{C_1}{A'_1}{D'_1}B'\] có ba cạnh OA1, OB1, OC1, đôi một vuông góc và bằng nhau. Vì thế hình hộp đó là hình lập phương có độ dài cạnh bằng 15. Suy ra độ dài đường chéo \[O{D'_1}\] của hình lập phương đó bằng \[15\sqrt 3 \].

Do chiếc đèn ở vị trí cân bằng nên \[\overrightarrow {{F_1}}  + \overrightarrow {{F_2}}  + \overrightarrow {{F_3}}  = \overrightarrow P \], ở đó \[\overrightarrow P \] là trọng lực tác dụng lên chiếc đèn. Suy ra trọng lượng của chiếc đèn là: \[\left| {\overrightarrow P } \right| = \left| {\overrightarrow {O{{D'}_1}} } \right| = 15\sqrt 3 \] (N).

Câu 3

Trọng tâm của tứ diện ABCD là một điểm I thoả mãn \[\overrightarrow {AI} {\rm{ }} = {\rm{ }}3\overrightarrow {IG} \], ở đó G là trọng tâm của tam giác BCD. Hãy tính khoảng cách từ trọng tâm của một khối rubik (đồng chất) hình tứ diện đều đến một mặt của nó, biết rằng chiều cao của khối rubik là 8 cm (H.2.30).
Trọng tâm của tứ diện ABCD là một điểm I thoả mãn AI = 3IG, ở đó G là trọng tâm của tam giác BCD (ảnh 1)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Một chiếc bàn cân đối hình chữ nhật được đặt trên mặt sàn nằm ngang, mặt bàn song song với mặt sàn và bốn chân bàn vuông góc với mặt sàn như Hình 2.29. Trọng lực tác dụng lên bàn (biểu thị bởi vectơ \[\overrightarrow a \]) phân tán đều qua bốn chân bàn và gây nên các phản lực từ mặt sàn lên các chân bàn (biểu thị bởi các vectơ b→, c→, d→ và e→.

a) Hãy chỉ ra mối quan hệ về phương và hướng của các vectơ a→, b→, c→, d→ và e→.

b) Giải thích vì sao các vectơ a→, b→, c→, d→ và e→ đôi một bằng nhau.

Một chiếc bàn cân đối hình chữ nhật được đặt trên mặt sàn nằm ngang, mặt bàn song song với mặt sàn (ảnh 1)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Một chiếc đèn chùm treo có khối lượng m = 5 kg được thiết kế với đĩa đèn được giữ bởi bốn đoạn xích SA, SB, SC, SD sao cho S.ABCD là hình chóp tứ giác đều có góc ASC = 60o (Hình 21).
Media VietJack

a) Sử dụng công thức \[\overrightarrow P  = m\overrightarrow g \] trong đó \[\overrightarrow g \] là vectơ gia tốc rơi tự do có độ lớn 10 m/s2, tìm độ lớn của trọng lực \[\overrightarrow P \] tác động lên chiếc đèn chùm.

b) Tìm độ lớn của lực căng cho mỗi sợi xích.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Một em nhỏ cân nặng m = 25 kg trượt trên cầu trượt dài 3,5 m. Biết rằng, cầu trượt có góc nghiêng so với phương nằm ngang là 30o (Hình 26).
Media VietJack

a) Tính độ lớn của trọng lực \[\overrightarrow P  = m\overrightarrow g \] tác dụng lên em nhỏ, cho biết vectơ gia tốc rơi tự do có độ lớn là g = 9,8 m/s2.

b) Cho biết công A (J) sinh bởi một lực \[\overrightarrow F \] có độ dịch chuyển \[\overrightarrow d \] được tính bởi công thức \[A = \overrightarrow F .\overrightarrow d \]. . Hãy tính công sinh bởi trọng lực \[\overrightarrow P \]  khi em nhỏ trượt hết chiều dài cầu trượt.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 7

Một lực tĩnh điện \[\overrightarrow F \] tác động lên điện tích điểm M  trong điện trường đều làm cho M dịch chuyển theo đường gấp khúc MNP (Hình vẽ). Biết q = 2 . 10−12 C, vectơ điện trường có độ lớn E = 1,8 . 105 N/C và d = MH = 5 mm. Tính công A sinh bởi lực tĩnh điện \[\overrightarrow F \].
Media VietJack

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Đăng ký

Bạn đã có tài khoản?

Khóa học 1 - 12
THPT
THCS
Phòng luyện đề
ĐGNL - ĐGTD
Tốt nghiệp THPT
Ôn vào 10
Ôn vào 6
Tài liệu
THPT
THCS
Tin Tuyển Sinh
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
Giấy chứng nhận ĐKKD số: 0108307822 do Sở KH & ĐT TP Hà Nội cấp lần đầu ngày 04/06/2018
© 2017 Vietjack72. All Rights Reserved.
zalo Nhắn tin Zalo Hỏi bài tập