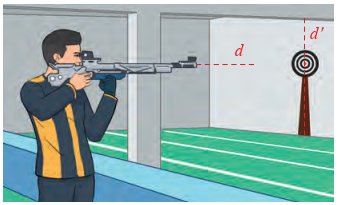
Trên phần mềm thiết kế chiếc cầu treo, cho đường thẳng \(d\) trên trụ cầu và đường thẳng \({d^\prime }\) trên sàn cầu có phương trình lần lượt là:
\(d:\left\{ {\begin{array}{*{20}{l}}{x = 0}\\{y = 0}\\{z = 50 + t}\end{array}{\rm{ và }}{d^\prime }:\left\{ {\begin{array}{*{20}{l}}{x = 20}\\{y = {t^\prime }}\\{z = 50.}\end{array}} \right.} \right.\)

Xét vị trí tương đối giữa \(d\) và \({d^\prime }\).
Trên phần mềm thiết kế chiếc cầu treo, cho đường thẳng \(d\) trên trụ cầu và đường thẳng \({d^\prime }\) trên sàn cầu có phương trình lần lượt là:
\(d:\left\{ {\begin{array}{*{20}{l}}{x = 0}\\{y = 0}\\{z = 50 + t}\end{array}{\rm{ và }}{d^\prime }:\left\{ {\begin{array}{*{20}{l}}{x = 20}\\{y = {t^\prime }}\\{z = 50.}\end{array}} \right.} \right.\)

Xét vị trí tương đối giữa \(d\) và \({d^\prime }\).
Quảng cáo
Trả lời:
Đường thẳng d và d' lần lượt có vectơ chí phương là \(\overrightarrow {{a_1}} = (0;0;1),\overrightarrow {{a_2}} = (0;1;0)\)
Ta có \(\overrightarrow {{a_1}} ,\overrightarrow {{a_2}} \) không cùng phương với nhau nên d và d' chéo nhau hoặc cắt nhau.
Ta xét hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{0 = 20}\\{0 = {t^\prime }}\\{50 + t = 50}\end{array}} \right.\) (vô nghiệm).
Vậy \(d\) và d' chéo nhau.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
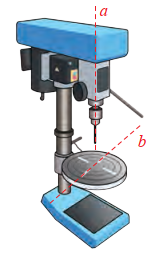
Đường thắng d và d' lần lượt có vectơ chỉ phương là \(\vec a = (1;0;0),\overrightarrow {{a^\prime }} = (0;0;3)\)
Ta có \(\vec a \cdot \overrightarrow {{a^\prime }} = 1.0 + 0.0 + 0.3 = 0\). Do đó d và d' vuông góc với nhau.
Lời giải
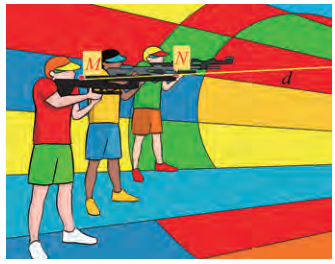
Ta có \(\overrightarrow {MN} = (0;1;0)\)
Đường thẳng MN đi qua \({\rm{M}}(3;3;1,5)\) và nhận \(\overrightarrow {MN} = (0;1;0)\) làm vectơ chỉ phương có phương trình là \(\left\{ {\begin{array}{*{20}{l}}{x = 3}\\{y = 3 + t}\\{z = 1,5}\end{array}} \right.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.