Cho tam giác \(ABC\) đều cạnh \(4cm\), đường trung tuyến \(AM\). Quay tam giác \(ABC\) quanh cạnh \(AM\). Tính diện tích toàn phần của hình nón tạo thành (đơn vị \(c{m^2}\)).
Câu hỏi trong đề: 50 bài tập Hình khối trong thực tiễn có lời giải !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Chọn C
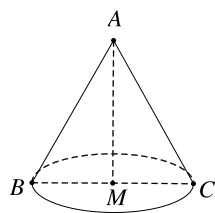
Xét tam giác \[ABC\] đều có \[AM\] vừa là đường trung tuyến, đường cao, đường phân giác.
Nên ta có \[MC = \frac{{BC}}{2} = \frac{4}{2} = 2(cm)\].
Khi quay tam giác \[ABC\] quanh cạnh \[AM\] ta được hình nón đỉnh \[A\], bán kính đáy là \[MC\], đường sinh \[AC\] và chiều cao \[AM\].
Diện tích toàn phần của hình nón là \[{S_{tp}} = \pi Rl + \pi {R^2} = \pi .MC.AC + \pi .M{C^2}\]
\[ = \pi .2.4 + \pi {.2^2} = 12\pi (c{m^2})\]
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Chọn D
Từ giả thiết ta có \[4\pi {R^2} = 2.\frac{4}{3}\pi {R^3} \Rightarrow {R^3} = \frac{3}{2}{R^2} \Rightarrow R = \frac{3}{2}\]
Lời giải
Chọn D
Gọi \[h\] và \[l\] theo thứ tự là chiều cao và đường sinh của hình nón. Khi đó:
Diện tích xung quanh của hình nón là \(\pi rl\).
Diện tích đáy của hình nón là \(\pi {r^2}\).
Vì hình nón có diện tích xung quanh gấp đôi diện tích đáy nên \(\pi rl = 2\pi {r^2} \Rightarrow l = 2r\).
Lại có \({l^2} = {h^2} + {r^2} \Rightarrow {h^2} = {l^2} - {r^2} = {\left( {2r} \right)^2} - {r^2} = 3{r^2} \Rightarrow h = r\sqrt 3 \).
Vậy thể tích của hình nón là \(V = \frac{1}{3}\pi {r^2}h = \frac{1}{3}\pi {r^2}.r\sqrt 3 = \frac{{\sqrt 3 }}{3}\pi {r^3}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo