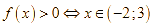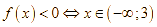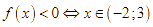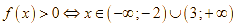Quảng cáo
Trả lời:
Ta có: ![]() .
.
Theo giả thiết: $\left( {m - 1} \right){x^2} + 2\left( {m - 1} \right)x + m - 3 \le 0,\,\,\,\forall x \in \,\,\,(*)$.
Trường hợp 1: ![]() . Thay vào (*): $1 - 3 \le 0,\forall x \in $ (đúng).
. Thay vào (*): $1 - 3 \le 0,\forall x \in $ (đúng).
Suy ra ![]() thỏa mãn.
thỏa mãn.
Trường hợp 2: ![]() .
.
(*) \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
\begin{array}{l}
a < 0\\
\Delta ' \le 0
\end{array}
\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
\begin{array}{l}
m - 1 < 0\\
{\left( {m - 1} \right)^2} - \left( {m - 1} \right)\left( {m - 3} \right) \le 0
\end{array}
\end{array}} \right.} \right.\\
\Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
\begin{array}{l}
m < 1\\
{m^2} - 2m + 1 - \left( {{m^2} - 4m + 3} \right) \le 0
\end{array}
\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
\begin{array}{l}
m < 1\\
2m - 2 \le 0
\end{array}
\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
\begin{array}{l}
m < 1\\
m \le 1
\end{array}
\end{array} \Leftrightarrow m < 1.} \right.} \right.} \right.
\end{array}$
Hợp hai kết quả trên, ta được ![]() . Mà
. Mà ![]() nên
nên ![]() .
.
Đáp án: 1.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Sách - Sổ tay kiến thức trọng tâm Vật lí 10 VietJack - Sách 2025 theo chương trình mới cho 2k9 ( 31.000₫ )
- Trọng tâm Lí, Hóa, Sinh 10 cho cả 3 bộ KNTT, CTST và CD VietJack - Sách 2025 ( 40.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Xét hàm số bậc hai ![]() .
.
Theo giả thiết, ta có: 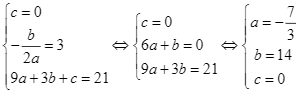 .
.
Vì vậy ![]() .
.
Ta cần xét: $y = - \frac{7}{3}{t^2} + 14t > 10$ hay $ - \frac{7}{3}{t^2} + 14t - 10 > 0$.
Đặt ![]() cho
cho ![]() .
.
Bảng xét dấu ![]() :
:
![]()
Kết luận: ![]() khi ${t_1} < t < {t_2}$ hay $\underbrace {\frac{{21 - \sqrt {231} }}{7}}_{ \approx 0,83} < t < \underbrace {\frac{{21 + \sqrt {231} }}{7}}_{ \approx 5,17}$.
khi ${t_1} < t < {t_2}$ hay $\underbrace {\frac{{21 - \sqrt {231} }}{7}}_{ \approx 0,83} < t < \underbrace {\frac{{21 + \sqrt {231} }}{7}}_{ \approx 5,17}$.
Vì ![]() nguyên nên
nguyên nên ![]() . Do vậy giá trị
. Do vậy giá trị ![]() thỏa mãn đề bài.
thỏa mãn đề bài.
Đáp án: 5.
Lời giải
Đáp án đúng là: C
Ta có ![]()
![]()
![]()
![]()
![]() ,
, ![]() .
.
Mà hệ số a = -1 < 0 nên ![]()
![]()
![]() .
.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.