Rút gọn biểu thức \(x\left( {x - y} \right) - y\left( {x + y} \right) + {x^2} + {y^2}\) ta được
A. \(2xy.\)
B. \(2{x^2}.\)
C. \( - 2xy.\)
D. \(2x\left( {x - y} \right).\)
Quảng cáo
Trả lời:
Đáp án đúng là: C
Ta có: \(x\left( {x - y} \right) - y\left( {x + y} \right) + {x^2} + {y^2} = {x^2} - xy - xy - {y^2} + {x^2} + {y^2} = - 2xy.\)
Do đó, chọn đáp án C.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Lời giải
a) Đúng
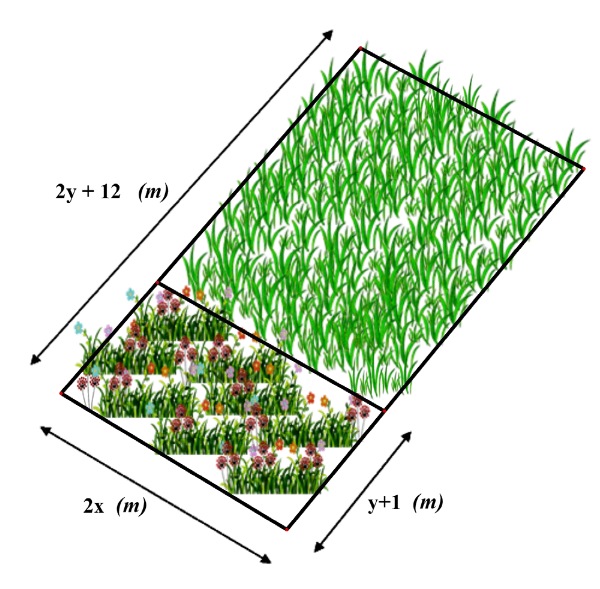
Diện tích của khu đất để trồng hoa là: \({S_1} = 2x\left( {y + 1} \right) = 2xy + 2x{\rm{ }}\left( {{{\rm{m}}^{\rm{2}}}} \right).\)
b) Sai
Chiều dài của khu đất dùng để trồng cỏ là: \(2y + 12 - y - 1 = y + 11{\rm{ }}\left( {\rm{m}} \right)\).
c) Sai
Diện tích của khu đất dùng để trồng cỏ là \({S_2} = \left( {y + 11} \right).2x = 2xy + 22x{\rm{ }}\left( {{{\rm{m}}^2}} \right)\)
d) Đúng
Diện tích của cả mảnh vườn là \(S = {S_1} + {S_2} = 2xy + 2x + 2xy + 22x = 4xy + 24x{\rm{ }}\left( {{{\rm{m}}^2}} \right)\).
Thay \(x = 4;y = 4\) vào \(S,\) ta được: \(S = 4 \cdot 4 \cdot 4 + 24 \cdot 4 = 160{\rm{ }}\left( {{{\rm{m}}^2}} \right)\).
Lời giải
Lời giải
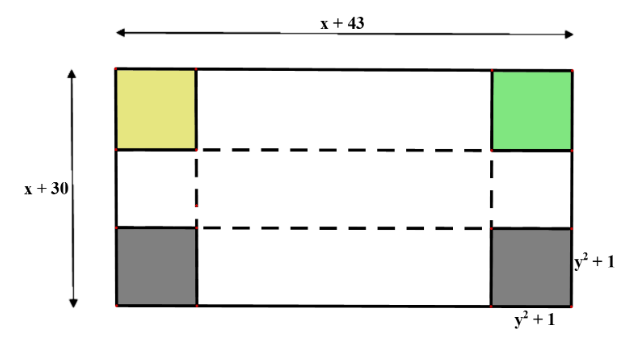
a) Đúng
Vì người ta cắt mỗi góc của tấm bìa một hình vuông cạnh \({y^2}{\rm{ + 1 }}\left( {{\rm{cm}}} \right)\) nên chiều dài của hình hộp chữ nhật là: \(x + 43 - 2\left( {{y^2} + 1} \right) = x - 2{y^2} + 41{\rm{ }}\left( {{\rm{cm}}} \right)\).
b) Đúng
Vì người ta cắt mỗi góc của tấm bìa một hình vuông cạnh \({y^2}{\rm{ + 1 }}\left( {{\rm{cm}}} \right)\) nên chiều rộng của hình hộp chữ nhật là: \(x + 30 - 2\left( {{y^2}{\rm{ + 1}}} \right) = x - 2{y^2} + 28{\rm{ }}\left( {{\rm{cm}}} \right).\)
c) Đúng
Biểu thức biểu thị diện tích xung quanh của hình hộp chữ nhật là:
\(S = 2\left( {x - 2{y^2} + 28 + x - 2{y^2} + 41} \right) \cdot \left( {{y^2} + 1} \right) = \left( {4x - 8{y^2} + 138} \right) \cdot \left( {{y^2} + 1} \right)\)
\( = 4x{y^2} - 8{y^4} + 138{y^2} + 4x - 8{y^2} + 138\)
\( = 4x{y^2} - 8{y^4} + 130{y^2} + 4x + 138{\rm{ }}\left( {{\rm{c}}{{\rm{m}}^2}} \right).\)
d) Sai.
Thay \(x = 16;y = 4\) vào \(S = 4x{y^2} - 8{y^4} + 130{y^2} + 4x + 138{\rm{ }}\left( {{\rm{c}}{{\rm{m}}^2}} \right)\) ta được:
\(S = 4 \cdot 16 \cdot {4^2} - 8 \cdot {4^4} + 130 \cdot {4^2} + 4 \cdot 4 + 138 = 1210{\rm{ }}\left( {{\rm{c}}{{\rm{m}}^2}} \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.