Cho ba số tự nhiên liên tiếp. Tích của hai số đầu nhỏ hơn tích của hai số sau là 50. Hỏi số nhỏ nhất có giá trị bằng bao nhiêu?

Bác Nam có một mảnh vườn hình chữ nhật. Bác chia mảnh vườn này ra làm hai khu đất hình chữ nhật: Khu thứ nhất dùng để trồng có. Khu thứ hai dùng để trồng hoa (Với các kích thước như hình vẽ)

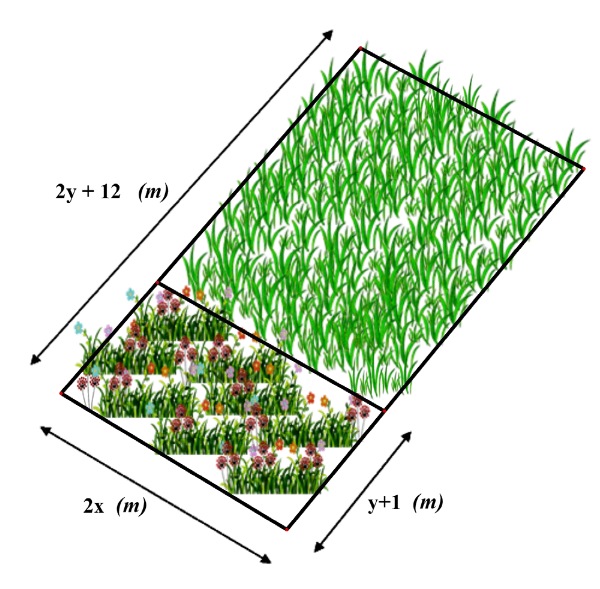
a) Diện tích của khu đất dùng để trồng hoa là \({S_1} = 2xy + 2x{\rm{ }}\left( {{{\rm{m}}^{\rm{2}}}} \right).\)

b) Chiều dài của khu đất dùng để trồng cỏ là \(y - 11{\rm{ }}\left( {\rm{m}} \right)\).

c) Diện tích khu đất dùng để trồng cỏ là \({S_2} = 2xy - 22x{\rm{ }}\left( {{{\rm{m}}^2}} \right)\).

d) Diện tích của cả mảnh vườn lớn hơn \(150{\rm{ }}{{\rm{m}}^2}\) khi \(x = 4;y = 4.\)

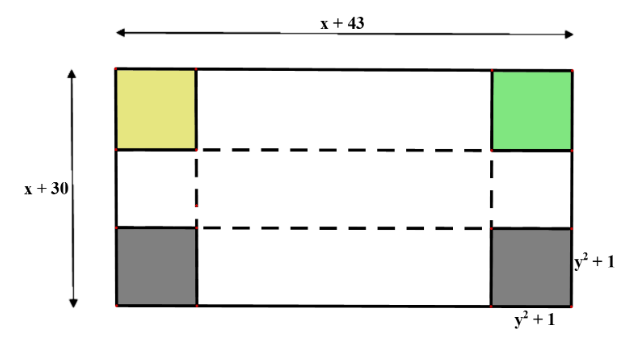
Một tấm bìa cứng hình chữ nhật có chiều dài \(x + 43{\rm{ }}\left( {{\rm{cm}}} \right),\) chiều rộng là \(x + 30{\rm{ }}\left( {{\rm{cm}}} \right).\) Người ta cắt ở mỗi góc của tấm bìa một hình vuông cạnh \({y^2}{\rm{ + 1 }}\left( {{\rm{cm}}} \right)\) (phần tô màu) và xếp phần còn lại thành một cái hộp không nắp.

a) Chiều dài của hình hộp chữ nhật là \(x - 2{y^2} + 41{\rm{ }}\left( {{\rm{cm}}} \right)\).

b) Chiều rộng của hình hộp chữ nhật là \(x - 2{y^2} + 28{\rm{ }}\left( {{\rm{cm}}} \right).\)

c) Biểu thức biểu thị diện tích xung quanh của hình hộp chữ nhật là

\(S = 4x{y^2} - 8{y^4} + 130{y^2} + 4x + 138{\rm{ }}\left( {{\rm{c}}{{\rm{m}}^2}} \right).\)

d) Diện tích xung quanh hình hộp chữ nhật có giá trị lớn hơn \({\rm{1250 }}\left( {{\rm{c}}{{\rm{m}}^2}} \right)\) khi \(x = 16;y = 4.\)

Một bức tường hình thang có cửa số hình tròn với các kích thước như hình dưới đây. (Đơn vị: mét, lấy \(\pi = 3,14\))

a) Diện tích toàn bộ bức tường là \(\frac{{3a.h}}{2}{\rm{ }}\left( {{{\rm{m}}^2}} \right)\).

b) Diện tích phần cửa kính hình tròn là \(2\pi {r^2}{\rm{ }}\left( {{{\rm{m}}^2}} \right)\).

c) Biểu thức biểu thị diện tích bức tường không tính phần cửa sổ là \(S = \frac{{3a.h}}{2} - 2\pi {r^2}{\rm{ }}\left( {{{\rm{m}}^2}} \right)\).

d) Khi \(a = 2{\rm{ }}\left( {\rm{m}} \right){\rm{, }}h = 3{\rm{ }}\left( {\rm{m}} \right){\rm{, }}r = 0,5{\rm{ }}\left( {\rm{m}} \right)\) thì diện tích bức tường hình thang lớn hơn \({\rm{7 }}\left( {{{\rm{m}}^2}} \right).\)

Khu vườn trồng mía của nhà bác Minh ban đầu có dạng một hình vuông, biết chu vi hình vuông là \(20{\rm{ }}\left( {\rm{m}} \right)\) sau đó được mở rộng bên phải thêm \(y{\rm{ }}\left( {\rm{m}} \right),\) phía dưới thêm \(8x{\rm{ }}\left( {\rm{m}} \right)\) nên mảnh vườn trở thành một hình chữ nhật (hình minh họa bên dưới).

a) Chiều rộng của khu vườn sau khi được mở rộng là \(y + 5{\rm{ }}\left( {\rm{m}} \right)\).

b) Chiều dài của khu vườn sau khi được mở rộng là \(8x + 5{\rm{ }}\left( {\rm{m}} \right)\).

c) Biểu thức biểu diễn diện tích của khu vườn sau khi mở rộng là \(8xy + 5y + 40x + 25{\rm{ }}\left( {{{\rm{m}}^2}} \right).\)

d) Diện tích của mảnh vườn sau khi được mở rộng có diện tích lớn hơn \(90{\rm{ }}\left( {{{\rm{m}}^2}} \right)\) khi \(x = 1;y = 2.\)

Biết \(x + y = 15\) và \(xy = - 100\). Tính giá trị của biểu thức \(B = {x^2} + {y^2}.\)

Cho đa thức \(A = 7x{y^2} + 4{y^2} - 7x{y^2} + 3 - 4y - 2\)

a) Đa thức thu gọn của đa thức \(A\) là \(A = 4{y^2} - 4y + 1\).

b) Bậc của đa thức \(A\) là bậc 3.

c) Giá trị của đa thức \(A\) không phụ thuộc vào biến \(x.\)

d) Giá trị của đa thức \(A\) tại \(y = - 1\) là 1.

Trong giờ học Mỹ thuật, bạn Hạnh dán lên trang vở hai hình cuông và một hình chữ nhật có độ dài hai cạnh góc vuông lần lượt là \(x{\rm{ }}\left( {{\rm{cm}}} \right),y{\rm{ }}\left( {{\rm{cm}}} \right)\) như hình dưới đây.

Tính tổng diện tích của hai hình vuông và tam giác vuông đó tại \(x = 3{\rm{ }}\left( {{\rm{cm}}} \right)\) và \(y = 5{\rm{ }}\left( {{\rm{cm}}} \right)\). (Kết quả viết dưới dạng số thập phân)