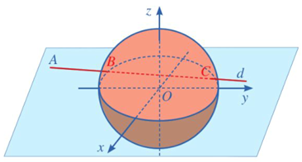
Biết rằng nếu vị trí M có vĩ độ và kinh độ tương ứng là thì có toạ độ . Tính khoảng cách trên mặt đất từ vị trí đến vị trí .
Biết rằng nếu vị trí M có vĩ độ và kinh độ tương ứng là thì có toạ độ . Tính khoảng cách trên mặt đất từ vị trí đến vị trí .
Quảng cáo
Trả lời:
Ta có
Suy ra:
Do đó
Vi P, Q thuộc mặt đất nên .
Do đó . Suy ra .
Mặt khác, đường tròn tâm, đi qua P, Q có bán kính 1 và chu vi là , nên cung nhỏ của đường tròn đó có độ dài xấp xỉ bằng .
Do 1 đơn vị dài trong không gian Oxyz tương ứng với 6371 km trên thực tế, nên khoảng cách trên mặt đất giữa hai vị trí P, Q xấp xỉ bằng 1,2983 6371 \( = 8271,4693(\;{\rm{km}})\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
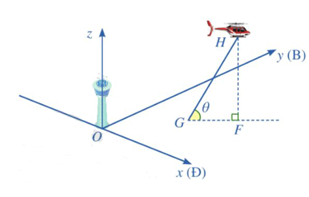
a) Phương trình tham số của đường thẳng d đi qua điểm \({\rm{A}}( - 688\); - 185; 8) và có vectơ chỉ phương \(\vec u = (91;75;0)\) là: \(\left\{ {\begin{array}{*{20}{l}}{x = - 688 + 91t}\\{y = - 185 + 75t{\rm{ (t là tham s?)}}{\rm{. }}}\\{z = 8}\end{array}} \right.\)
Gọi B là vị trí sớm nhất mà máy bay xuất hiện trên màn hình ra đa.
Vi B \(B\) d nên B(- 688 + 91t; - 185 + 75t; 8).
\(B\) là vị trí sớm nhất mà máy bay xuất hiện trên màn hình ra đa khi \({\rm{OB}} = 417\), tức là \(\sqrt {{{( - 688 + 91t)}^2} + {{( - 185 + 75t)}^2} + {8^2}} = 417\)\( \Leftrightarrow 13906{t^2} - 152966t + 333744 = 0\)\( \Leftrightarrow t = 3{\rm{ hay }}t = 8.{\rm{ }}\)
\( + {\rm{ Vì }} = 3,{\rm{ ta có }}B( - 415;40;8){\rm{. }}\)
+ Với \( = 3\), ta có \(B( - 415;40;8)\).
Khi đó \({\rm{AB}} = \sqrt {{{( - 415 + 688)}^2} + {{(40 + 185)}^2}} \approx 353,77\).
+ Với \({\rm{t}} = 8\), ta có \({\rm{B}}( - 88;415;8)\). Khi đó \(AB = \sqrt {{{( - 88 + 688)}^2} + {{(415 + 185)}^2}} \approx 848,53\).
Vi \(353,77 < 848,53\) nên tọa độ vị trí sớm nhất mà máy bay xuất hiện trên màn hình ra đa là \(( - 415;40;8)\).
b) Gọi H là vị trí mà máy bay bay gần đài kiểm soát không lưu nhất. Khi đó, khoảng OH phải ngắn nhất, điều này xảy ra khi và chỉ khi \({\rm{OH}} \bot {\rm{d}}\).
Vi H \( \in \) d nên \(H( - 688 + 91t\) '; - \(185 + 75\) t'; 8).
Ta có \(\overrightarrow {OH} = ( - 688 + 91t; - 185 + 75t;8)\).
\({\rm{OH}} \bot {\rm{d}} \Leftrightarrow \overrightarrow {OH} \bot \vec u \Leftrightarrow \overrightarrow {OH} \cdot \vec u = 0\)
\( \Leftrightarrow ( - 688 + 91t) \cdot 91 + ( - 185 + 75t) \cdot 75 + 8 \cdot 0 = 0\)
\( \Leftrightarrow 13906{{\rm{t}}^\prime } - 76483 = 0 \Leftrightarrow {{\rm{t}}^\prime } = \frac{{11}}{2}\). Suy ra H \(\left( { - \frac{{375}}{2};\frac{{455}}{2};8} \right)\).
Khoảng cách giữa máy bay và đài kiểm soát không lưu lúc đó là:
\({\rm{OH}} = \sqrt {{{\left( { - \frac{{375}}{2}} \right)}^2} + {{\left( {\frac{{455}}{2}} \right)}^2} + {8^2}} \approx 294,92(\;{\rm{km}}){\rm{. }}\)
c) Từ kết quả ở câu a), ta suy ra toạ độ của vị trí mà máy bay ra khỏi màn hình ra đa là \(( - 88;415;8)\).
Lời giải
a) Mặt cầu \((S)\) có phương trình
\({(x - 32)^2} + {(y - 50)^2} + {(z - 10)^2} = 109\)
nên có tâm \(I(32;50;10)\) và bán kính \(R = \sqrt {109} \).
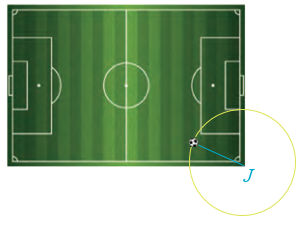
b) Trong không gian Oxyz, mặt sân có phương trình \(z = 0\) trùng với mặt phẳng tọa độ \((Oxy)\), suy ra hình chiếu vuông góc của điểm \(I(32;50;10)\) xuống mặt sân có toạ độ \(J(32;50;0)\).
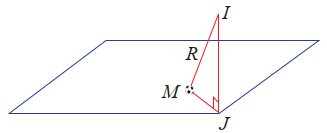
c) Trong tam giác vuông IJM, ta có \(IJ = 10,IM = {\rm{R}}\), suy ra
\(JM = \sqrt {I{M^2} - I{J^2}} = \sqrt {109 - 100} = 3.\)
Vậy khoảng cách từ vị trí \(M\) của quả bóng đến điểm \(J\) là 3 m .
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.