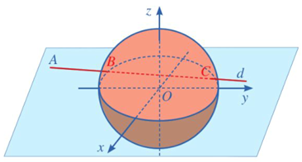
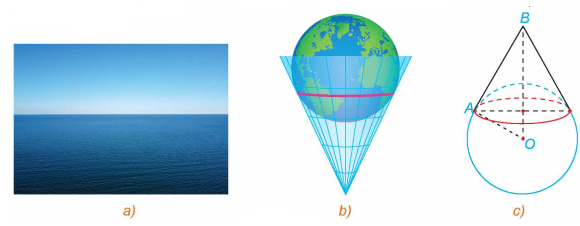
Né́u đứng trước biển và nhìn ra xa, người ta sẽ thấy một đường giao giữa mặt biển và bầu trời, đó là đường chân trời đối với người quan sát (H.5.45a). Về mặt Vật lí, đường chân trời là đường giới hạn phần Trái Đất mà người quan sát có thể nhìn thấy được (phần còn lại bị chính Trái Đất che khuất). Ta có thể hình dung rằng, nếu người quan sát ở tại đỉnh của một chiếc nón và Trái Đát được "thả" vào trong chiếc nón đó, thì đường chân trời trong trường hợp này là đường chạm giữa Trái Đất và chiếc nón (H.5.45b). Trong mô hình toán học, đường chân trời đối với người quan sát tại vị trí \(B\) là tập hợp những điểm \(A\) nằm trên bề mặt Trái Đất sao cho , với O là tâm Trái Đất (H.5.45c). Trong không gian Oxyz, giả sử bề mặt Trái Đất \((S)\) có phương trình \({x^2} + {y^2} + {z^2} = 1\) và người quan sát ở vị trí \(B(1,1; - 1)\).
Gọi \(A\) là một vị trí bất kì trên đường chân trời đối với người quan sát ở vị trí \(B\). Tính khoảng cách AB.
Né́u đứng trước biển và nhìn ra xa, người ta sẽ thấy một đường giao giữa mặt biển và bầu trời, đó là đường chân trời đối với người quan sát (H.5.45a). Về mặt Vật lí, đường chân trời là đường giới hạn phần Trái Đất mà người quan sát có thể nhìn thấy được (phần còn lại bị chính Trái Đất che khuất). Ta có thể hình dung rằng, nếu người quan sát ở tại đỉnh của một chiếc nón và Trái Đát được "thả" vào trong chiếc nón đó, thì đường chân trời trong trường hợp này là đường chạm giữa Trái Đất và chiếc nón (H.5.45b). Trong mô hình toán học, đường chân trời đối với người quan sát tại vị trí \(B\) là tập hợp những điểm \(A\) nằm trên bề mặt Trái Đất sao cho , với O là tâm Trái Đất (H.5.45c). Trong không gian Oxyz, giả sử bề mặt Trái Đất \((S)\) có phương trình \({x^2} + {y^2} + {z^2} = 1\) và người quan sát ở vị trí \(B(1,1; - 1)\).

Gọi \(A\) là một vị trí bất kì trên đường chân trời đối với người quan sát ở vị trí \(B\). Tính khoảng cách AB.
Quảng cáo
Trả lời:
Mặt cầu \((S)\) có tâm \(O(0;0;0)\) và \({\rm{R}} = 1\).
Ta có \(A \in (S)\) nên \(OA = 1\).
\({\rm{ Có }}OB = \sqrt {{1^2} + {1^2} + {{( - 1)}^2}} = \sqrt 3 \)
Xét tam giác BOA vuông tại \(O\) có: \(AB = \sqrt {O{B^2} - O{A^2}} = \sqrt {3 - 1} = \sqrt 2 \)
Vậy khoảng cách AB là \(\sqrt 2 \).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Phương trình tham số của đường thẳng d đi qua điểm \({\rm{A}}( - 688\); - 185; 8) và có vectơ chỉ phương \(\vec u = (91;75;0)\) là: \(\left\{ {\begin{array}{*{20}{l}}{x = - 688 + 91t}\\{y = - 185 + 75t{\rm{ (t là tham s?)}}{\rm{. }}}\\{z = 8}\end{array}} \right.\)
Gọi B là vị trí sớm nhất mà máy bay xuất hiện trên màn hình ra đa.
Vi B \(B\) d nên B(- 688 + 91t; - 185 + 75t; 8).
\(B\) là vị trí sớm nhất mà máy bay xuất hiện trên màn hình ra đa khi \({\rm{OB}} = 417\), tức là \(\sqrt {{{( - 688 + 91t)}^2} + {{( - 185 + 75t)}^2} + {8^2}} = 417\)\( \Leftrightarrow 13906{t^2} - 152966t + 333744 = 0\)\( \Leftrightarrow t = 3{\rm{ hay }}t = 8.{\rm{ }}\)
\( + {\rm{ Vì }} = 3,{\rm{ ta có }}B( - 415;40;8){\rm{. }}\)
+ Với \( = 3\), ta có \(B( - 415;40;8)\).
Khi đó \({\rm{AB}} = \sqrt {{{( - 415 + 688)}^2} + {{(40 + 185)}^2}} \approx 353,77\).
+ Với \({\rm{t}} = 8\), ta có \({\rm{B}}( - 88;415;8)\). Khi đó \(AB = \sqrt {{{( - 88 + 688)}^2} + {{(415 + 185)}^2}} \approx 848,53\).
Vi \(353,77 < 848,53\) nên tọa độ vị trí sớm nhất mà máy bay xuất hiện trên màn hình ra đa là \(( - 415;40;8)\).
b) Gọi H là vị trí mà máy bay bay gần đài kiểm soát không lưu nhất. Khi đó, khoảng OH phải ngắn nhất, điều này xảy ra khi và chỉ khi \({\rm{OH}} \bot {\rm{d}}\).
Vi H \( \in \) d nên \(H( - 688 + 91t\) '; - \(185 + 75\) t'; 8).
Ta có \(\overrightarrow {OH} = ( - 688 + 91t; - 185 + 75t;8)\).
\({\rm{OH}} \bot {\rm{d}} \Leftrightarrow \overrightarrow {OH} \bot \vec u \Leftrightarrow \overrightarrow {OH} \cdot \vec u = 0\)
\( \Leftrightarrow ( - 688 + 91t) \cdot 91 + ( - 185 + 75t) \cdot 75 + 8 \cdot 0 = 0\)
\( \Leftrightarrow 13906{{\rm{t}}^\prime } - 76483 = 0 \Leftrightarrow {{\rm{t}}^\prime } = \frac{{11}}{2}\). Suy ra H \(\left( { - \frac{{375}}{2};\frac{{455}}{2};8} \right)\).
Khoảng cách giữa máy bay và đài kiểm soát không lưu lúc đó là:
\({\rm{OH}} = \sqrt {{{\left( { - \frac{{375}}{2}} \right)}^2} + {{\left( {\frac{{455}}{2}} \right)}^2} + {8^2}} \approx 294,92(\;{\rm{km}}){\rm{. }}\)
c) Từ kết quả ở câu a), ta suy ra toạ độ của vị trí mà máy bay ra khỏi màn hình ra đa là \(( - 88;415;8)\).
Lời giải
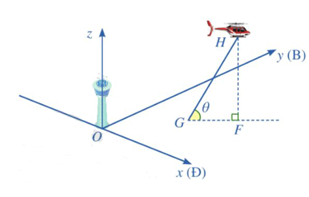
a) Ta có góc \(\theta \) mà đường bay tạo với phương ngang chính là góc giữa đường thẳng GH và mặt phẳng \(({\rm{Oxy}})\).
Tại thời điểm \({\rm{t}} = 0\) thì \(\overrightarrow {{r_0}} = (1;0,5;0)\). Trực thăng cất cánh từ điểm \(G\) nên \({\rm{G}}(1;0,5;0)\).
Tại thời điểm \({\rm{t}} = 1\), trực thăng bay đến vị trí K thuộc đường thẳng GH với \({\rm{K}}(2\); 2,5 ; 2 ).
Đường thẳng GH có vectơ chỉ phương \(\overrightarrow {GK} = (1;2;2)\) và mặt phẳng \(({\rm{Oxy}})\) có vectơ pháp tuyến \(\vec k = (0;0;1)\)
Ta có \(\sin ({\rm{GH}},({\rm{Oxy}})) = \frac{{|1 \cdot 0 + 2 \cdot 0 + 2 \cdot 1|}}{{\sqrt {{1^2} + {2^2} + {2^2}} \cdot \sqrt {{0^2} + {0^2} + {1^2}} }} = \frac{2}{3}\).
Suy ra . Vậy
b) Gọi \({{\rm{K}}^\prime }\) là hình chiếu của điểm K lên mặt phẳng (Oxy). Khi đó K (2; 2,5 ; 0).
Vi F là hình chiếu của điểm H lên mặt phẳng (Oxy) nên \({{\rm{K}}^\prime } \in {\rm{GF}}\).
Do đó đường thẳng GF có vectơ chỉ phương là \(\overrightarrow {G{K^\prime }} = (1;2;0)\).
Phương trình tham số của đường thẳng GF là \(\left\{ {\begin{array}{*{20}{l}}{x = 1 + {t^\prime }}\\{y = 0,5 + 2{t^\prime }{\rm{ ( }}{{\rm{t}}^\prime }{\rm{ là tham }}}\\{z = 0}\end{array}} \right.\) số).
c) Trực thăng bay vào mây ở độ cao 2 km , tức là vị trí điểm mà trực thăng bắt đầu đi vào đám mây có cao độ \(z = 2\), khi đó \(2t = 2\), suy ra \(t = 1\).
Vậy tọa độ điểm mà trực thăng bắt đầu đi vào đám mây là \((2;2,5;2)\).
d) Ta có \({\rm{H}}(1 + {\rm{t}};0,5 + 2{\rm{t}};2{\rm{t}})\). Khi đó, \(\overrightarrow {HM} = (4 - t;4 - 2t;3 - 2t)\).
Đường thẳng GH có vectơ chỉ phương \(\overrightarrow {GK} = (1;2;2)\).
HM vuông góc với đường bay GH khi \(\overrightarrow {HM} \bot \overrightarrow {GK} \Leftrightarrow \overrightarrow {HM} \cdot \overrightarrow {GK} = 0\)
\( \Leftrightarrow (4 - t) \cdot 1 + (4 - 2t) \cdot 2 + (3 - 2t) \cdot 2 = 0 \Leftrightarrow t = 2.{\rm{ }}\)
Vậy \({\rm{t}} = 2\) thì HM vuông góc với đường bay GH .
Khi đó, khoảng cách từ đỉnh núi đến máy bay trực thăng là:
\(HM = \sqrt {{{(4 - 2)}^2} + {{(4 - 2 \cdot 2)}^2} + {{(3 - 2 \cdot 2)}^2}} = \sqrt 5 (\;{\rm{km}})\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.