khoahoc.vietjack.com
Giảm 50% Kích hoạt VIP
khoahoc.vietjack.com
Kích hoạt VIP Đăng nhập
Tạo VIP
  2. Lớp 12
  3. Toán

Câu hỏi:

25/08/2025 397 Lưu

PHẦN II. TRẢ LỜI NGẮN

Nếu một vật có khối lượng m(kg) thì lực hấp dẫn \(\overrightarrow P \) của Trái Đất tác dụng lên vật được xác định theo công thức \(\overrightarrow P  = m\overrightarrow g \), trong đó \(\overrightarrow g \) là gia tốc rơi tự do có độ lớn g = 9,8 m/s2. Tính độ lớn của lực hấp dẫn của Trái Đất tác dụng lên một quả táo có khối lượng 105 gam (làm tròn kết quả đến hàng phần trăm).

Xem lời giải

Câu hỏi trong đề: 20 câu trắc nghiệm Toán 12 Chân trời sáng tạo Bài 1. Vectơ và các phép toán trong không gian (Đúng sai - Trả lời ngắn) có đáp án !!

Flashcard Bắt Đầu Thi Giao bài

Quảng cáo

Trả lời:

verified Giải bởi Vietjack

Đổi 105 g = 0,105 kg.

Độ lớn của lực hấp dẫn của Trái Đất tác dụng lên một quả táo là:

\(\left| {\overrightarrow P } \right| = m\left| {\overrightarrow g } \right| = 0,105.9,8 = 1,029N \approx 1,03N\).

Trả lời: 1,03.

Đang tải chế độ Học...

Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay

ĐẶC QUYỀN VIP

Đăng ký VIP để học và luyện thi không giới hạn

Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.

  • Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
  • Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
  • Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
  • Tải xuống đề thi [DOCX] với đầy đủ đáp án
  • Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
  • Bao gồm tất cả các bậc từ Tiểu học đến Đại học
  • Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
  • Đăng ký ngay
Avatar

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Trong không gian, cho tứ diện S.ABC có SA = SB = SC = AB = AC = 2, \(BC = 2\sqrt 2 \). Tính \(\overrightarrow {SC} .\overrightarrow {AB} \).

Lời giải

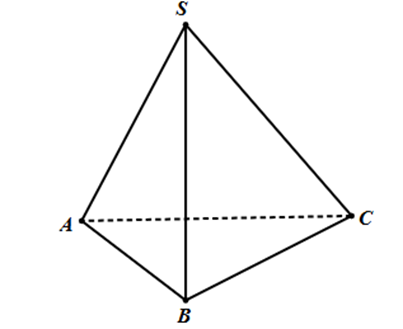
Trong không gian, cho tứ diện S.ABC có SA = SB = SC = AB = AC = 2, \(BC = 2\sqrt 2 \). Tính \(\overrightarrow {SC} .\overrightarrow {AB} \). (ảnh 1)

Vì BC2 = SB2 + SC2 nên DSBC vuông cân tại S.

Mặt khác SA = AC = SC = 2 Þ DSAC là tam giác đều.

Ta có \(\overrightarrow {SC} .\overrightarrow {AB}  = \overrightarrow {SC} .\left( {\overrightarrow {SB}  - \overrightarrow {SA} } \right) = \overrightarrow {SC} .\overrightarrow {SB}  - \overrightarrow {SC} .\overrightarrow {SA} \)\( = 0 - \left| {\overrightarrow {SC} } \right|.\left| {\overrightarrow {SA} } \right|.\cos \widehat {ASC} =  - 2.2.\cos 60^\circ  = \frac{{ - {2^2}}}{2} =  - 2\).

Vậy \(\overrightarrow {SC} .\overrightarrow {AB}  =  - 2\).

Trả lời: −2.

Câu 2

Trong không gian, cho tứ diện \(ABCD\). Ta có \[\overrightarrow {AB} \, + \,\overrightarrow {CD} \] bằng

A. \[\overrightarrow {AD} \, + \,\overrightarrow {BC} \].                                     

B. \[\overrightarrow {DA} \, + \,\overrightarrow {CB} \] .

C. \[\overrightarrow {DA} \, + \,\overrightarrow {BC} \].  
D. \[\overrightarrow {AD} \, + \,\overrightarrow {CB} \].

Lời giải

Theo quy tắc ba điểm, ta có: \[\overrightarrow {AB\,} \, = \overrightarrow {AD} \, + \,\overrightarrow {DB} \]

Do đó:\[\overrightarrow {AB} \, + \,\overrightarrow {CD} \, = \,\overrightarrow {AD} \, + \,\overrightarrow {DB} \, + \,\overrightarrow {CD} \]

         \( = \overrightarrow {AD} \, + \left( {\,\overrightarrow {DB} \, + \,\overrightarrow {CD} } \right)\) \( = \,\overrightarrow {AD} \, + \left( {\,\,\overrightarrow {CD} \, + \,\overrightarrow {DB} } \right)\)\( = \,\overrightarrow {AD} \, + \,\overrightarrow {CB} \).

Câu 3

Cho tứ diện đều \[ABCD\] có cạnh bằng \[4\]. Tính giá trị tích vô hướng \[\overrightarrow {AB} \left( {\overrightarrow {AB}  - \overrightarrow {CA} } \right)\].

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Cho hình chóp tứ giác đều S.ABCD có độ dài tất cả các cạnh đều bằng a.

a) Tứ giác ABCD là hình vuông.

b) Tam giác SBD cân tại S.

c) \(\left( {\overrightarrow {SB} ,\overrightarrow {BD} } \right) = 45^\circ \).

d) \(\overrightarrow {SB} .\overrightarrow {BD}  =  - {a^2}\).

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Cho tứ diện ABCD. Gọi M và N lần lượt là trung điểm của AB, CD và G là trung điểm MN.

a) \(\overrightarrow {GA}  + \overrightarrow {GB}  + \overrightarrow {GC}  + \overrightarrow {GD}  = \overrightarrow 0 \).

b) \(\overrightarrow {MA}  + \overrightarrow {MB}  + \overrightarrow {MC}  + \overrightarrow {MD}  = 4\overrightarrow {MG} \).

c) \(\overrightarrow {MN}  = \frac{1}{2}\left( {\overrightarrow {AB}  + \overrightarrow {CD} } \right)\).

d)\(2\overrightarrow {MN}  = \overrightarrow {AC}  + \overrightarrow {BD} \).

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = 1, AD = 2, AA' = 3. Gọi M là một điểm trên đoạn CC' sao cho CM = 2MC'.

a) \(\overrightarrow {AA'}  = \frac{3}{2}\overrightarrow {CM} \).

b) \(\cos \left( {\overrightarrow {AM} ,\overrightarrow {A'C'} } \right) = \frac{2}{3}\).

c) \(\overrightarrow {AM}  = \overrightarrow {AB}  + \overrightarrow {AD}  + \frac{1}{3}\overrightarrow {AA'} \).

d) \(\overrightarrow {AM} .\overrightarrow {B'D}  = 0\).

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 7

Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Trong các mệnh đề sau mệnh đề nào là mệnh đề sai?

 A. \(\overrightarrow {SA}  + \overrightarrow {SB}  + \overrightarrow {SC}  + \overrightarrow {SD}  = 4\overrightarrow {SO} \).           

B. \(\overrightarrow {SA}  - \overrightarrow {SB}  + \overrightarrow {SC}  - \overrightarrow {SD}  = \overrightarrow 0 \).

C. \(\overrightarrow {SA}  + \overrightarrow {SB}  + \overrightarrow {SC}  + \overrightarrow {SD}  = \overrightarrow 0 \).     
D. \(\overrightarrow {OA}  + \overrightarrow {OB}  + \overrightarrow {OC}  + \overrightarrow {OD}  = \overrightarrow 0 \).

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Đăng ký

Bạn đã có tài khoản?

Khóa học 1 - 12
THPT
THCS
Phòng luyện đề
ĐGNL - ĐGTD
Tốt nghiệp THPT
Ôn vào 10
Ôn vào 6
Tài liệu
THPT
THCS
Tin Tuyển Sinh
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
Giấy chứng nhận ĐKKD số: 0108307822 do Sở KH & ĐT TP Hà Nội cấp lần đầu ngày 04/06/2018
© 2017 Vietjack37. All Rights Reserved.
zalo Nhắn tin Zalo Hỏi bài tập