khoahoc.vietjack.com
Giảm 50% Kích hoạt VIP
khoahoc.vietjack.com
Kích hoạt VIP Đăng nhập
Tạo VIP
  2. Lớp 12
  3. Toán

Câu hỏi:

25/08/2025 345 Lưu

PHẦN II. TRẢ LỜI NGẮN

Một chiếc máy đo đạc trắc địa được đặt trên một giá đỡ ba chân với điểm đặt S(0; 0; 4) và các điểm tiếp xúc với mặt đất của ba chân lần lượt là \(A\left( { - 2;0;0} \right),B\left( {1;\sqrt 3 ;0} \right),C\left( {1; - \sqrt 3 ;0} \right)\). Biết rằng trọng lực tác dụng lên chiếc máy có độ lớn 30 N và được phân bố thành ba lực \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} ,\overrightarrow {{F_3}} \) có độ lớn bằng nhau như hình. Tính tích vô hướng của \(\overrightarrow {{F_1}} .\overrightarrow {{F_2}} \).

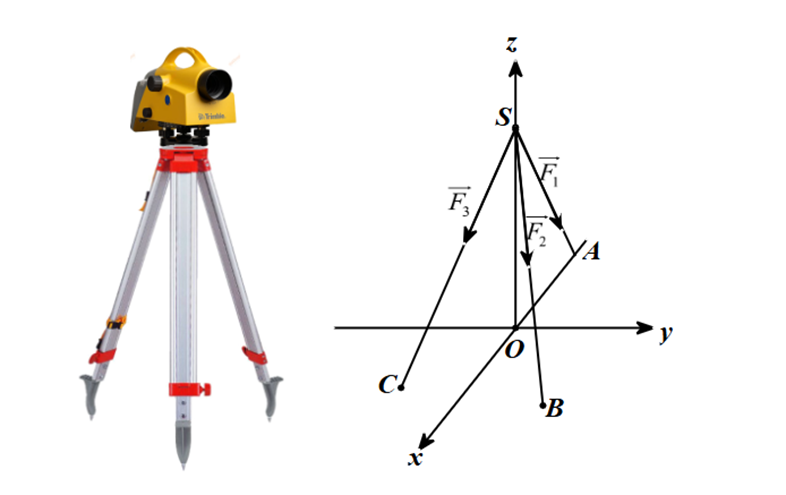
Tính tích vô hướng của \(\overrightarrow {{F_1}} .\overrightarrow {{F_2}} \). (ảnh 1)

Xem lời giải

Câu hỏi trong đề: 20 câu trắc nghiệm Toán 12 Chân trời sáng tạo Bài 3. Biểu thức tọa độ của các phép toán vectơ (Đúng sai - Trả lời ngắn) có đáp án !!

Flashcard Bắt Đầu Thi Giao bài

Quảng cáo

Trả lời:

verified Giải bởi Vietjack

Ta có \(\overrightarrow {SA}  = \left( { - 2;0; - 4} \right),\overrightarrow {SB}  = \left( {1;\sqrt 3 ; - 4} \right),\overrightarrow {SC}  = \left( {1; - \sqrt 3 ; - 4} \right)\) \( \Rightarrow SA = SB = SC = \sqrt {20} \).

Lại có \(\overrightarrow {AB}  = \left( {3;\sqrt 3 ;0} \right),\overrightarrow {AC}  = \left( {3; - \sqrt 3 ;0} \right),\overrightarrow {BC}  = \left( {0; - 2\sqrt 3 ;0} \right)\) \( \Rightarrow AB = AC = BC = \sqrt {12} \).

Do đó hình chóp S.ABC đều có đường cao là SO = 4 với O(0; 0; 0) là trọng tâm tam giác ABC.

Mặt khác, \(\overrightarrow {{F_1}}  = k\overrightarrow {SA}  = \left( { - 2k;0; - 4k} \right),\overrightarrow {{F_2}}  = k\overrightarrow {SB}  = \left( {k;\sqrt 3 k; - 4k} \right),\overrightarrow {{F_3}}  = k\overrightarrow {SC}  = \left( {k; - \sqrt 3 k; - 4k} \right)\)

\( \Rightarrow \overrightarrow {{F_1}}  + \overrightarrow {{F_2}}  + \overrightarrow {{F_3}}  = \left( {0;0; - 12k} \right)\).

Mà \(\overrightarrow {{F_1}}  + \overrightarrow {{F_2}}  + \overrightarrow {{F_3}}  = \overrightarrow P  = \left( {0;0; - 30} \right)\) nên \( - 12k =  - 30 \Leftrightarrow k = \frac{5}{2}\).

Suy ra \(\overrightarrow {{F_1}}  = \left( { - 5;0; - 10} \right),\overrightarrow {{F_2}}  = \left( {\frac{5}{2};\frac{{5\sqrt 3 }}{2}; - 10} \right)\).

Vậy \(\overrightarrow {{F_1}} .\overrightarrow {{F_2}}  = \frac{{175}}{2} = 87,5\).

Trả lời: 87,5.

Đang tải chế độ Học...

Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay

ĐẶC QUYỀN VIP

Đăng ký VIP để học và luyện thi không giới hạn

Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.

  • Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
  • Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
  • Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
  • Tải xuống đề thi [DOCX] với đầy đủ đáp án
  • Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
  • Bao gồm tất cả các bậc từ Tiểu học đến Đại học
  • Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
  • Đăng ký ngay
Avatar

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Trong không gian Oxyz, cho hai điểm A(1; 2; 1), B(2; −1; 3) và điểm M(a; b; 0) sao cho MA2 + MB2 nhỏ nhất. Tính giá trị của a + b.

Lời giải

Ta có MA2 + MB2 = (1 – a)2 + (2 – b)2 + 12 + (2 – a)2 + (−1 – b)2 + 32

= 2a2 – 6a + 2b2 – 2b + 20 = \(2{\left( {a - \frac{3}{2}} \right)^2} + 2{\left( {b - \frac{1}{2}} \right)^2} + 15 \ge 15\).

Đẳng thức xảy ra khi \(a = \frac{3}{2};b = \frac{1}{2}\). Khi đó a + b = 2.

Trả lời: 2.

Câu 2

Hình vẽ sau mô tả vị trí của máy bay vào thời điểm 9h30 phút. Biết các đơn vị trên hình tính theo đơn vị km.

a) Máy bay đang ở độ cao 9 km. b) Tọa độ của máy bay (300; 150; 9). (ảnh 1)

a) Máy bay đang ở độ cao 9 km.

b) Tọa độ của máy bay (300; 150; 9).

c) Phi công để máy bay ở chế độ tự động với vận tốc theo hương đông là 750 km/h, độ cao không đổi. Biết rằng gió thổi theo hướng đông với vận tốc 10 m/s. Giả sử vận tốc và hướng gió không đổi thì lúc 10 giờ 30 phút máy bay ở tọa độ (150; 1086; 9).

d) Sau khi bay đến vị trí lúc 10 giờ 30 phút thì máy bay bay ngược lại với vận tốc 800 km/h với độ cao không đổi, biết lúc đó trời lặng gió thì lúc 11 giờ máy bay ở tọa độ (686; 150; 9).

Lời giải

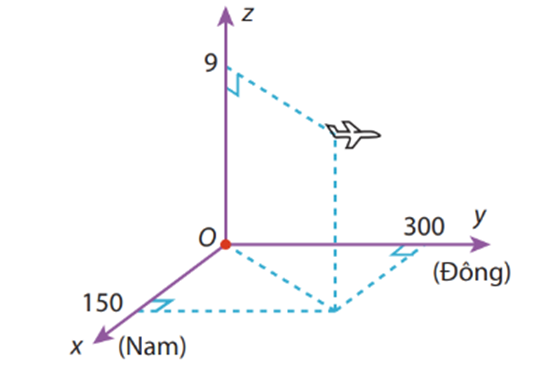
. a) Dựa vào hình vẽ ta thấy máy bay đang ở độ cao 9 km.

b) Máy bay ở tọa độ (150; 300;9).

c) Vận tốc gió 10 m/s = 36 km/h.

Quãng đường máy bay bay được là 750 + 36 = 786 km.

Do đó tọa độ của máy bay là (150; 1086; 9).

d) Quãng đường máy bay bay được là \(800.\frac{1}{2} = 400\) km. Do đó tọa độ máy bay là (150; 686; 9).

Đáp án: a) Đúng;   b) Sai;   c) Đúng;   d) Sai.

Câu 3

Trong không gian với hệ tọa độ Oxyz, cho A(1; 2; 0); B(−1; 0; 3). Tìm tọa độ điểm M thuộc tia Ox sao cho tam giác ABM vuông tại M.
A. M(1; 0; 0). 
B. M(−1; 0; 0).           
C. M(0; 0; 1). 
D. M(0; 0; −1).

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Trong không gian chọn hệ trục tọa độ cho trước, đơn vị đo lấy kilômét, ra đa phát hiện một máy bay chiến đấu của Nga di chuyển với vận tốc và hướng không đổi từ điểm M(600; 400; 20) đến điểm N(800; 500; 30) trong 30 phút. Nếu máy bay tiếp tục giữ nguyên vận tốc và hướng bay thì tốc độ của máy bay sau 15 phút tiếp theo là P(a; b; c). Tính a + b + c.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Cho các điểm A(1; −1; 0), B(0; 2; 0), C(2; 1; 3) và M là điểm thỏa mãn hệ thức \(\overrightarrow {MA}  - \overrightarrow {MB}  + \overrightarrow {MC}  = \overrightarrow 0 \). Khi đó điểm M có tọa độ là
A. (3; 2; 3).     
B. (3; −2; −3). 
C. (3; −2; 3).   
D. (3; 2; −3).

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Trong không gian Oxyz, cho hai điểm A(1; 3; 2) và B(3; −1; 4). Tọa độ vectơ \(\overrightarrow u  = 2\overrightarrow {BA}  - \overrightarrow {OB} \).

A. \(\overrightarrow u  = \left( { - 7;7; - 8} \right)\). 

B. \(\overrightarrow u  = \left( { - 7;3; - 8} \right)\).                                     
C. \(\overrightarrow u  = \left( { - 7;5; - 8} \right)\).   
D. \(\overrightarrow u  = \left( { - 7;9; - 8} \right)\).

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 7

Trong phần mềm mô phỏng việc điều khiển drone giao hàng trong không gian Oxyz, một drone giao hàng đang ở tọa độ A(1; 0; 1) di chuyển đến địa điểm nhận hàng là B(4; 4; 6). Mỗi đơn vị trên phần mềm bằng 1 km ngoài thực tế. Biết tốc độ của drone là 80 km/h. Giả sử rằng từ vị trí giao hàng và nhận hàng không gặp chướng ngại vật, sức cản gió khống đáng kể để drone bay theo đường thẳng. Thời gian drone bay từ vị trí ban đến đến địa điểm giao hàng mất bao nhiêu phút (làm tròn đến hàng phần mười).

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Đăng ký

Bạn đã có tài khoản?

Khóa học 1 - 12
THPT
THCS
Phòng luyện đề
ĐGNL - ĐGTD
Tốt nghiệp THPT
Ôn vào 10
Ôn vào 6
Tài liệu
THPT
THCS
Tin Tuyển Sinh
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
Giấy chứng nhận ĐKKD số: 0108307822 do Sở KH & ĐT TP Hà Nội cấp lần đầu ngày 04/06/2018
© 2017 Vietjack37. All Rights Reserved.
zalo Nhắn tin Zalo Hỏi bài tập