khoahoc.vietjack.com
Kích hoạt VIP
khoahoc.vietjack.com
Kích hoạt VIP Đăng nhập
Tạo VIP
  2. Lớp 12
  3. Toán

Câu hỏi:

25/08/2025 258 Lưu

Trong một căn phòng dạng hình hộp chữ nhật với chiều dài 8m, rộng 6m và cao 4m có 1 cây quạt treo tường. Cây quạt A treo chính giữa bức tường và cách trần 1m, cây quạt B treo chính giữa bức tường và cách trần 1,5m. Chọn hệ trục tọa độ Oxyz như hình vẽ bên dưới (đơn vị mét). Giả sử \(\overrightarrow {AB}  = \left( {a;b;c} \right)\). Tính a + b + c.

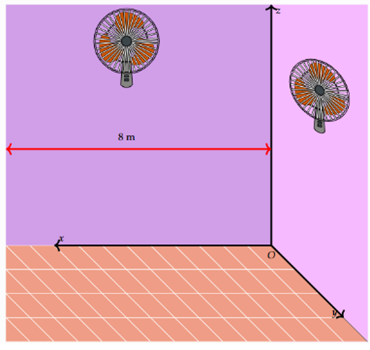
Tính a + b + c. (ảnh 1)

Xem lời giải

Câu hỏi trong đề: 20 câu trắc nghiệm Toán 12 Chân trời sáng tạo Bài 3. Biểu thức tọa độ của các phép toán vectơ (Đúng sai - Trả lời ngắn) có đáp án !!

Flashcard Bắt Đầu Thi Giao bài

Quảng cáo

Trả lời:

verified Giải bởi Vietjack

Theo đề ta có \(A\left( {4;0;3} \right);B\left( {0;3;\frac{5}{2}} \right)\).

Khi đó \(\overrightarrow {AB}  = \left( { - 4;3; - \frac{1}{2}} \right)\).

Do đó \(a + b + c =  - 1,5\).

Trả lời: −1,5.

\(\overrightarrow v  = \left( {1; - 5; - 3} \right)\)

Đang tải chế độ Học...

Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay

Các sản phẩm khác của Vietjack:
  1. Combo 3 khóa học Toán - Văn - Anh lớp 1-12 chỉ với 250k
  2. Phòng luyện 1000 đề VIP Đgnl các trường ĐHQGHN, Tp.HCM, Bách Khoa, tốt nghiệp THPT chỉ với 399k
  3. Mã giảm giá 20% sản phẩm sách VietJack trên Shopee mall
Avatar

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Trong không gian Oxyz, cho hai điểm A(1; 2; 1), B(2; −1; 3) và điểm M(a; b; 0) sao cho MA2 + MB2 nhỏ nhất. Tính giá trị của a + b.

Lời giải

Ta có MA2 + MB2 = (1 – a)2 + (2 – b)2 + 12 + (2 – a)2 + (−1 – b)2 + 32

= 2a2 – 6a + 2b2 – 2b + 20 = \(2{\left( {a - \frac{3}{2}} \right)^2} + 2{\left( {b - \frac{1}{2}} \right)^2} + 15 \ge 15\).

Đẳng thức xảy ra khi \(a = \frac{3}{2};b = \frac{1}{2}\). Khi đó a + b = 2.

Trả lời: 2.

Câu 2

Hình vẽ sau mô tả vị trí của máy bay vào thời điểm 9h30 phút. Biết các đơn vị trên hình tính theo đơn vị km.

a) Máy bay đang ở độ cao 9 km. b) Tọa độ của máy bay (300; 150; 9). (ảnh 1)

a) Máy bay đang ở độ cao 9 km.

b) Tọa độ của máy bay (300; 150; 9).

c) Phi công để máy bay ở chế độ tự động với vận tốc theo hương đông là 750 km/h, độ cao không đổi. Biết rằng gió thổi theo hướng đông với vận tốc 10 m/s. Giả sử vận tốc và hướng gió không đổi thì lúc 10 giờ 30 phút máy bay ở tọa độ (150; 1086; 9).

d) Sau khi bay đến vị trí lúc 10 giờ 30 phút thì máy bay bay ngược lại với vận tốc 800 km/h với độ cao không đổi, biết lúc đó trời lặng gió thì lúc 11 giờ máy bay ở tọa độ (686; 150; 9).

Lời giải

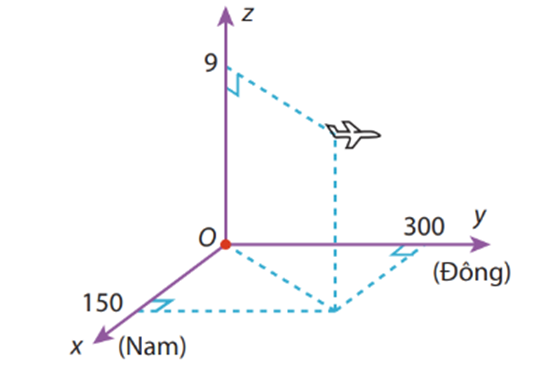
. a) Dựa vào hình vẽ ta thấy máy bay đang ở độ cao 9 km.

b) Máy bay ở tọa độ (150; 300;9).

c) Vận tốc gió 10 m/s = 36 km/h.

Quãng đường máy bay bay được là 750 + 36 = 786 km.

Do đó tọa độ của máy bay là (150; 1086; 9).

d) Quãng đường máy bay bay được là \(800.\frac{1}{2} = 400\) km. Do đó tọa độ máy bay là (150; 686; 9).

Đáp án: a) Đúng;   b) Sai;   c) Đúng;   d) Sai.

Câu 3

Trong không gian với hệ tọa độ Oxyz, cho A(1; 2; 0); B(−1; 0; 3). Tìm tọa độ điểm M thuộc tia Ox sao cho tam giác ABM vuông tại M.
A. M(1; 0; 0). 
B. M(−1; 0; 0).           
C. M(0; 0; 1). 
D. M(0; 0; −1).

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Trong không gian chọn hệ trục tọa độ cho trước, đơn vị đo lấy kilômét, ra đa phát hiện một máy bay chiến đấu của Nga di chuyển với vận tốc và hướng không đổi từ điểm M(600; 400; 20) đến điểm N(800; 500; 30) trong 30 phút. Nếu máy bay tiếp tục giữ nguyên vận tốc và hướng bay thì tốc độ của máy bay sau 15 phút tiếp theo là P(a; b; c). Tính a + b + c.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Cho các điểm A(1; −1; 0), B(0; 2; 0), C(2; 1; 3) và M là điểm thỏa mãn hệ thức \(\overrightarrow {MA}  - \overrightarrow {MB}  + \overrightarrow {MC}  = \overrightarrow 0 \). Khi đó điểm M có tọa độ là
A. (3; 2; 3).     
B. (3; −2; −3). 
C. (3; −2; 3).   
D. (3; 2; −3).

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Trong không gian Oxyz, cho hai điểm A(1; 3; 2) và B(3; −1; 4). Tọa độ vectơ \(\overrightarrow u  = 2\overrightarrow {BA}  - \overrightarrow {OB} \).

A. \(\overrightarrow u  = \left( { - 7;7; - 8} \right)\). 

B. \(\overrightarrow u  = \left( { - 7;3; - 8} \right)\).                                     
C. \(\overrightarrow u  = \left( { - 7;5; - 8} \right)\).   
D. \(\overrightarrow u  = \left( { - 7;9; - 8} \right)\).

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 7

Trong phần mềm mô phỏng việc điều khiển drone giao hàng trong không gian Oxyz, một drone giao hàng đang ở tọa độ A(1; 0; 1) di chuyển đến địa điểm nhận hàng là B(4; 4; 6). Mỗi đơn vị trên phần mềm bằng 1 km ngoài thực tế. Biết tốc độ của drone là 80 km/h. Giả sử rằng từ vị trí giao hàng và nhận hàng không gặp chướng ngại vật, sức cản gió khống đáng kể để drone bay theo đường thẳng. Thời gian drone bay từ vị trí ban đến đến địa điểm giao hàng mất bao nhiêu phút (làm tròn đến hàng phần mười).

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Đăng ký

Bằng cách đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của VietJack.

Bạn đã có tài khoản?

Khóa học 1 - 12
THPT
THCS
Phòng luyện đề
ĐGNL - ĐGTD
Tốt nghiệp THPT
Ôn vào 10
Ôn vào 6
Tài liệu
THPT
THCS
Tin Tuyển Sinh
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
Giấy chứng nhận ĐKKD số: 0108307822 do Sở KH & ĐT TP Hà Nội cấp lần đầu ngày 04/06/2018
© 2017 Vietjack37. All Rights Reserved.
zalo Nhắn tin Zalo Hỏi bài tập