Trong không gian với hệ tọa độ \[Oxyz\], với \[\overrightarrow i ,\overrightarrow j ,\overrightarrow k \] lần lượt là các vecto đơn vị trên các trục \[Ox,\,\,Oy,\,\,Oz.\] Tính tọa độ của vecto \[\overrightarrow i + \overrightarrow j - \overrightarrow k .\]

PHẦN II.  Câu trắc nghiệm đúng sai. Học sinh trả lời từ câu 11 đến câu 14. Trong mỗi ý a), b), c), d) ở mỗi câu, học sinh chọn đúng hoặc sai.

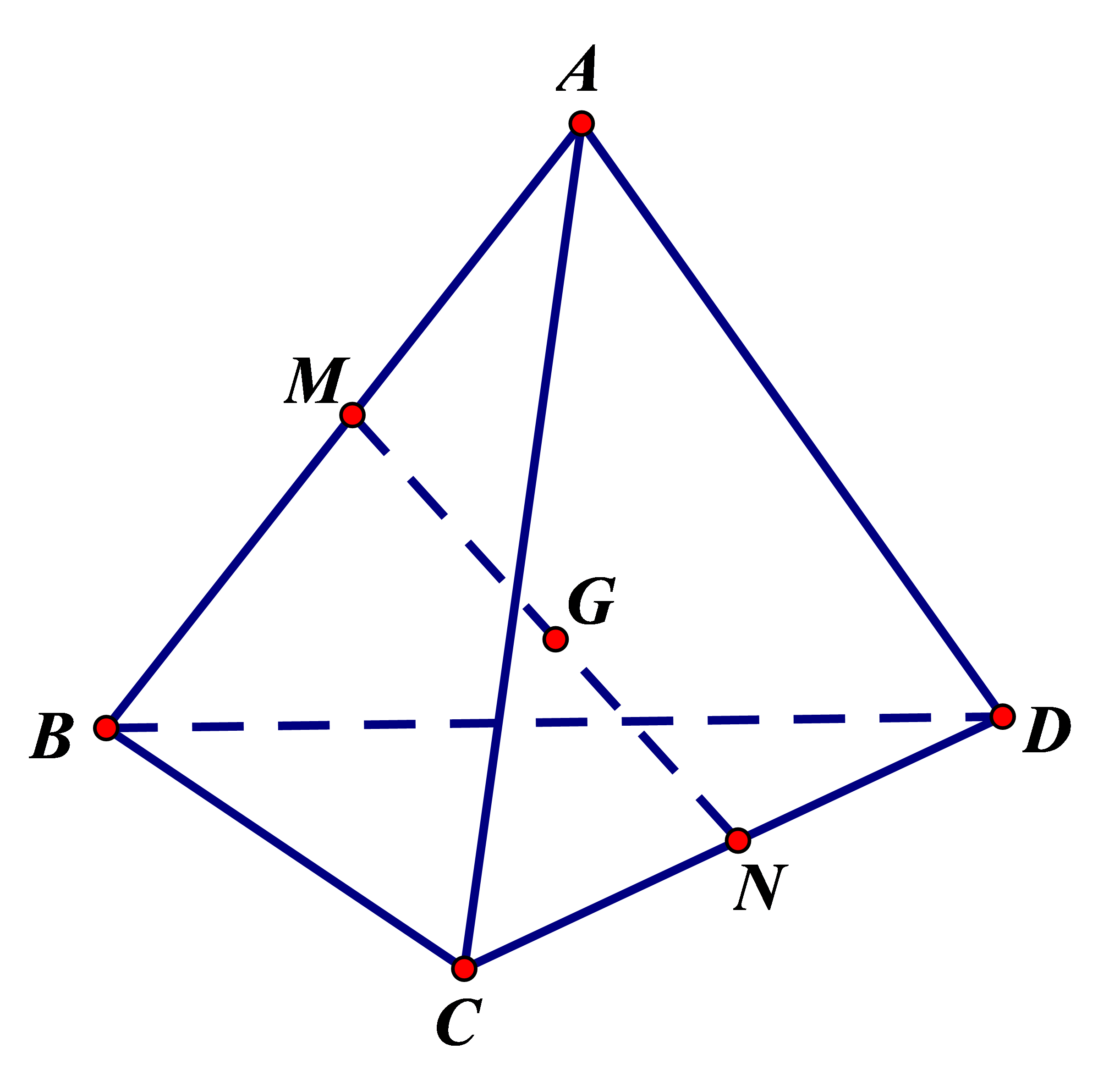
Cho tứ diện \(ABCD\). Gọi \(M,N,G\) lần lượt là trung điểm của \(AB\), \(CD\), \(MN\).

a)  \(\overrightarrow {MA} + \overrightarrow {MB} = \overrightarrow 0 \).

b)  \(\overrightarrow {MC} + \overrightarrow {MD} = 2\overrightarrow {MN} \).

c)  \(\overrightarrow {GA} + \overrightarrow {GB} = \overrightarrow {GC} + \overrightarrow {GD} \).

d)  \(\overrightarrow {AD} + \overrightarrow {BC} = \overrightarrow {MN} \).

Trong không gian \(Oxyz\), cho tam giác \(ABC\) có \(A(1;2;4),B(4; - 2;1),C(3;4;7)\)    

a)  Toạ độ trọng tâm \(G\) của tam giác \(ABC\) là \(G\left( {\frac{8}{3};\frac{4}{3};4} \right)\).

b)  Toạ độ điểm \(D\) sao cho \(ABCD\) là hình bình hành là \(D\left( {0;8;10} \right)\).

c)  Toạ độ điểm \(M\) thuộc đoạn \(AB\) sao cho \(MB = 2MA\) là \(M\left( {2;\frac{2}{3};3} \right)\).

d)  \(\cos \widehat {BAC} = \frac{{11\sqrt 2 }}{{34}}\).

Cho lập phương \(ABCD.A'B'C'D'\)có cạnh bằng \(a.\)

a)  \(\overrightarrow {AB}  + \overrightarrow {AD}  + \overrightarrow {AA'}  = \overrightarrow {AC'} \).

b)  \(\left( {\overrightarrow {AC} ,\overrightarrow {D'A'} } \right) = {45^0}\).

c)  \(\overrightarrow {BD} .\overrightarrow {A'C'}  = 0\).

d)  \(\overrightarrow {AC'} .\overrightarrow {AB}  = \frac{3}{2}{a^2}\).

Trong không gian \(Oxyz\), cho \(\overrightarrow a  = \left( {1;2; - 3} \right)\), \(\overrightarrow b  = \left( {3;1;5} \right)\).

a)  \(\overrightarrow a  + \overrightarrow b  = \left( {4;3;2} \right)\).

b)  \(2\overrightarrow a  - 3\overrightarrow b  = \left( { - 7;1;21} \right)\).

c)  \(\overrightarrow a .\overrightarrow b  = 10\).

d)  \(\cos \left( {\overrightarrow a ,\overrightarrow b } \right) =  - \frac{{\sqrt {10} }}{7}\).