PHẦN III. Câu trắc nghiệm trả lời ngắn.
Trong không gian \(Oxyz\), cho hai vectơ \(\vec a = \left( {1;2; - 3} \right);\vec b = \left( { - 1; - 2;z} \right)\). Tìm giá trị \(z\) sao cho \(\vec a + \vec b = \overrightarrow 0 \).
PHẦN III. Câu trắc nghiệm trả lời ngắn.
Trong không gian \(Oxyz\), cho hai vectơ \(\vec a = \left( {1;2; - 3} \right);\vec b = \left( { - 1; - 2;z} \right)\). Tìm giá trị \(z\) sao cho \(\vec a + \vec b = \overrightarrow 0 \).
Quảng cáo
Trả lời:
Trả lời: \(z = 3.\)
Ta có: \(\vec a + \vec b = \left( {0;0;z - 3} \right).\)
\(\vec a + \vec b = \overrightarrow 0 \Leftrightarrow z - 3 = 0 \Leftrightarrow z = 3.\)
Vậy \(z = 3.\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Trả lời : \(1,15\)
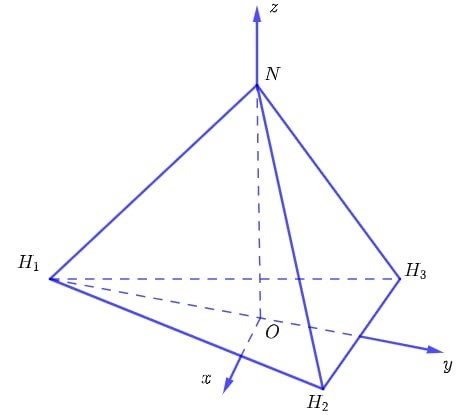
Gọi \(a = {H_1}{H_2}\) là khoảng cách giữa hai nguyên tử hydrogen , khi đó độ dài \(O{H_1} = \frac{{\sqrt 3 }}{2}{H_1}{H_2} \Leftrightarrow \sqrt 3 = \frac{{\sqrt 3 a}}{2} \Rightarrow a = 2\).
Giả sử góc tạo bởi liên kết \(H - N - H,\) có hai cạnh là hai đoạn thẳng nối \(N\) với hai trong ba điểm \({H_1},\,{H_2},\,{H_3}\) là góc \(\widehat {{H_2}N{H_3}} = {120^ \circ }\)
Gọi \(x\) là khoảng cách giữa nguyên tử nitrogen với mỗi nguyên tử hydrogen, khi đó \(N{H_2} = x\)
Áp dụng định lý cosin ta có:
\({H_2}{H_3} = N{H_2}^2 + N{H_3}^2 - 2.N{H_2}.N{H_3}.\cos \widehat {{H_2}N{H_3}}\)\( \Leftrightarrow 4 = {x^2} + {x^2} - 2{x^2}\cos {120^ \circ } \Rightarrow {x^2} = \frac{4}{3} \Rightarrow x = \frac{{2\sqrt 3 }}{3} \approx 1,15 \cdot \)
Lời giải
a) Đúng.
Ta có \[\overrightarrow x = \overrightarrow a + \overrightarrow b = (3;4;2)\] .
b) Sai.
Ta có \[\overrightarrow y = \overrightarrow a + \overrightarrow c = (5;2; - 1)\].
c) Sai.
Ta có \[\overrightarrow z = \overrightarrow b + \overrightarrow c = (6;2; - 5)\].
d) Đúng.
Ta có \(\overrightarrow k = \overrightarrow a + \overrightarrow b + \overrightarrow c = (7;4; - 2)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.