Tính thể tích \(V\) của phần vật thể giới hạn bởi hai mặt phẳng \(x = 0,\,x = 1\), có thiết diện bị cắt bởi mặt phẳng vuông góc với trục \(Ox\) tại điểm có hoành độ \(x\,\left( {0 \le x \le 1} \right)\) là một tam giác đều có cạnh bằng \(x\).

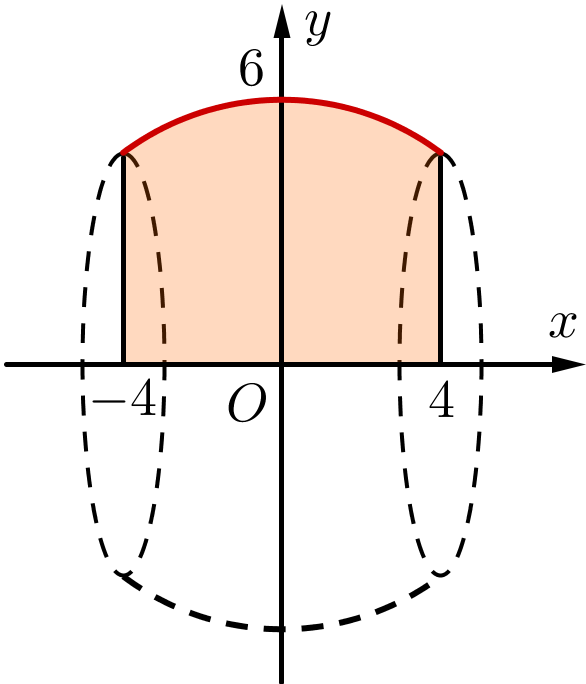
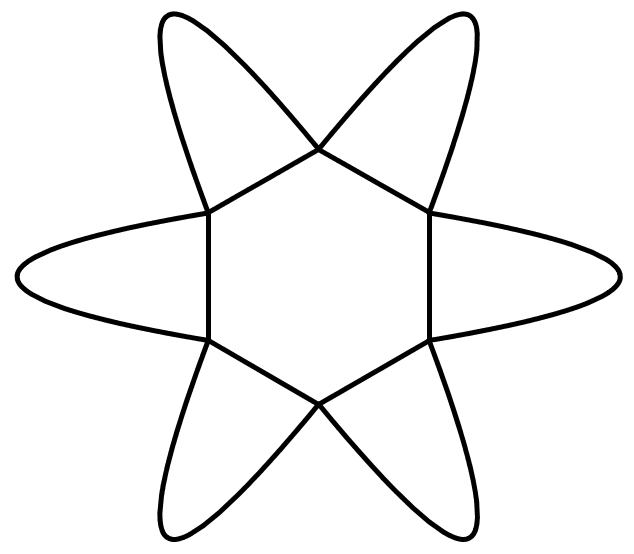
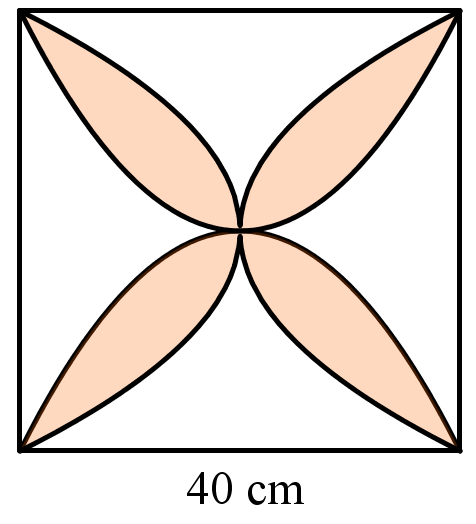
Chọn hệ tọa độ như hình vẽ (1 đơn vị trên trục bằng \(10\,{\rm{cm}} = 1\,{\rm{dm}}\)), các cánh hoa tạo bởi các đường parabol có phương trình \(y = \frac{{{x^2}}}{3}\), \(y =  - \frac{{{x^2}}}{3}\),\(x =  - \frac{{{y^2}}}{3}\),\(x = \frac{{{y^2}}}{3}\).

Diện tích một cánh hoa (nằm trong góc phần tư thứ nhất) bằng diện tích hình phẳng giới hạn bởi hai đồ thị hàm số\(y = \frac{{{x^2}}}{3}\),\(y = \sqrt {3x} \) và hai đường thẳng \(x = 0;x = 3\).

Do đó diện tích một cánh hoa bằng: \(\int\limits_0^3 {\left( {\sqrt {3x}  - \frac{{{x^2}}}{3}} \right){\rm{d}}x} \) \[ = 3\left( {{\rm{d}}{{\rm{m}}^{\rm{2}}}} \right) = 300\left( {{\rm{c}}{{\rm{m}}^{\rm{2}}}} \right)\].

Đáp án: 300.

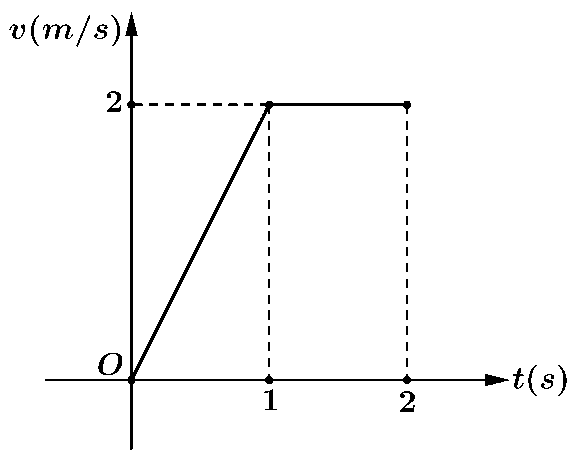
a) Sai. Dựa vào đồ thị \(v\left( t \right)\).

b) Đúng. Trong \(3\) giây đầu tiên, vận tốc của chuyển động là \(v\left( t \right) = 11\,\left( {{\rm{m/s}}} \right)\).

Do đó quãng đường chất điểm chuyển động trong \(3\)giây đầu tiên là: \({S_1} = \int\limits_0^3 {11{\rm{d}}t} \,\,\left( {\rm{m}} \right)\).

c) Đúng. Trong khoảng thời gian từ \(8\) đến \(15\) giây, đồ thị \(v\left( t \right)\) là một đường thẳng đi qua hai điểm \(\left( {8;21} \right)\) và \(\left( {15;0} \right)\). Ta có: \(v\left( t \right) = at + b\).

Từ giả thiết ta có hệ: \(\left\{ {\begin{array}{*{20}{c}}{8a + b = 21}\\{15a + b = 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{a =  - 3}\\{b = 45}\end{array}} \right.\).

Do đó \(v\left( t \right) =  - 3t + 45\,\,\left( {8 \le t \le 15} \right)\).

Quãng đường chất điểm đi được trong khoảng thời gian này là:

\({S_2} = \int\limits_8^{15} {\left( { - 3t + 45} \right){\rm{d}}t}  =  - \frac{{3{t^2}}}{2}\left| {\begin{array}{*{20}{c}}{15}\\8\end{array}} \right. + 45t\left| {\begin{array}{*{20}{c}}{15}\\8\end{array}} \right. = \frac{{147}}{2} = 73,5\,\left( {\rm{m}} \right)\).

d) Sai. Trong khoảng thời gian từ \(3\) đến \(8\) giây đồ thị \(v\left( t \right)\) là một Parabol đi qua các điểm có tọa độ lần lượt là  \(\left( {3;11} \right),\left( {5;3} \right),\left( {8;21} \right)\) có phương trình dạng: \(v\left( t \right) = a{t^2} + bt + c\).

Từ giả thiết ta có: \(\left\{ {\begin{array}{*{20}{c}}{9a + 3b + c = 11}\\{25a + 5b + c = 3}\\{64a + 8b + c = 21}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{a = 2}\\{b =  - 20}\\{c = 53}\end{array}} \right.\)

Do đó: \(v\left( t \right) = 2{t^2} - 20t + 53\,\,\left( {3 \le t \le 8} \right)\).

Quãng đường chất điểm đi được trong khoảng thời gian này là:

\[{S_3} = \int\limits_3^8 {v\left( t \right){\rm{d}}t}  = \int\limits_3^8 {\left( {2{t^2} - 20t + 53} \right){\rm{d}}t = \,\,} \left( {\frac{{2{t^3}}}{3} - 10{t^2} + 53t} \right)\left| {\begin{array}{*{20}{c}}8\\3\end{array}} \right. = \frac{{115}}{3}\,\,\,\left( {\rm{m}} \right)\].

Vận tốc trung bình của chất điểm trong khoảng thời gian này là: \({v_{tb}} = \frac{{{S_3}}}{5} = \frac{{23}}{3} \approx 7,67\,\left( {{\rm{m/s}}} \right)\).