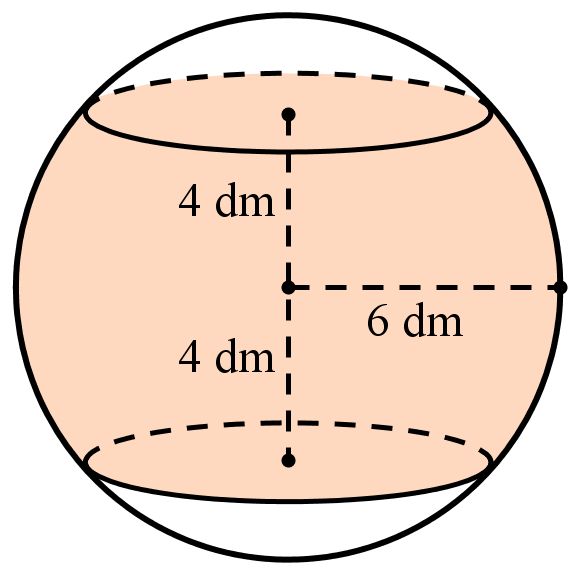
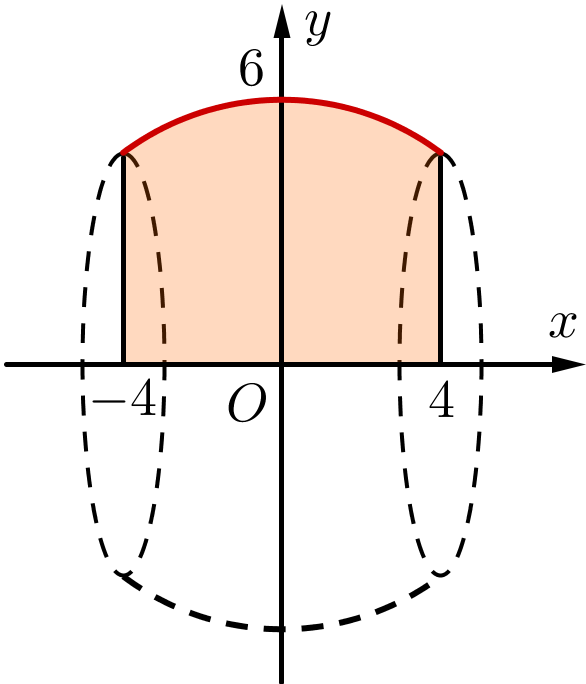
Trên cửa sổ có dạng hình chữ nhật, họa sĩ thiết kế logo hình con cá cho một doanh nghiệp kinh doanh hải sản. Logo là hình phẳng giới hạn bởi hai parabol với các kích thước được cho trong hình sau (đơn vị trên mỗi trục toạ độ là decimét).

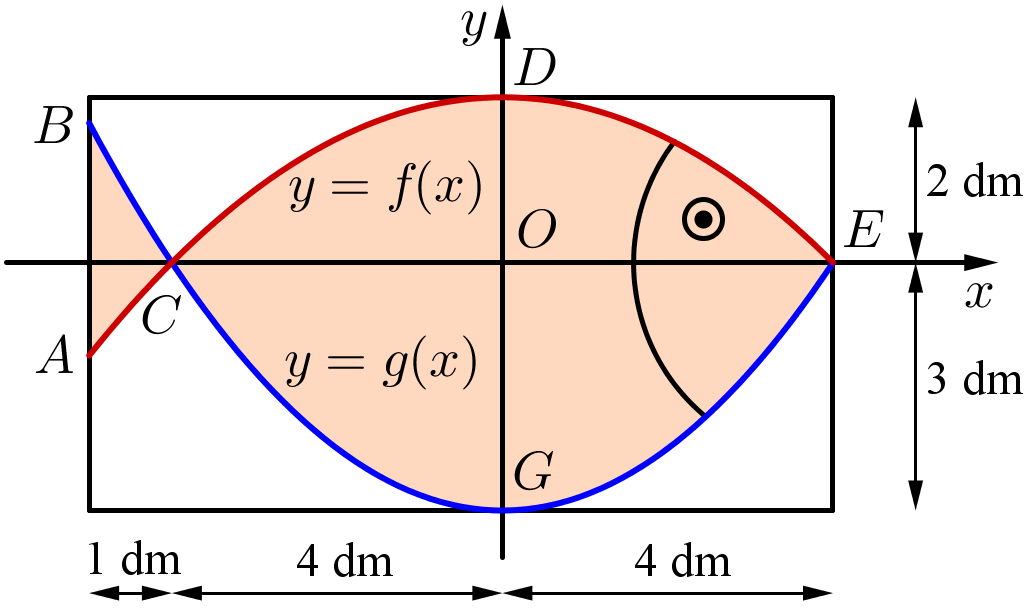
a) Lập phương trình các parabol \[y = f\left( x \right)\] và \[y = g\left( x \right)\].

b) Tính diện tích của logo.

c) Logo chỉ cho phép 50% lượng ánh sáng đi qua. Lượng ánh sáng đi qua toàn bộ cửa sổ sau khi làm logo sẽ giảm bao nhiêu phần trăm (làm tròn kết quả đến hàng phần mười)?

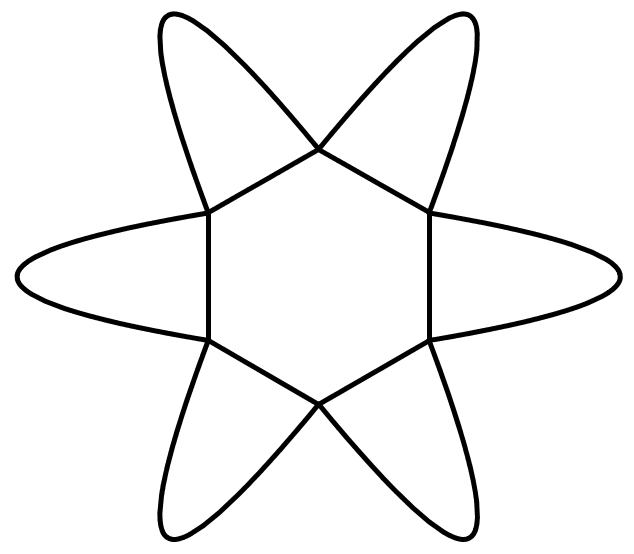
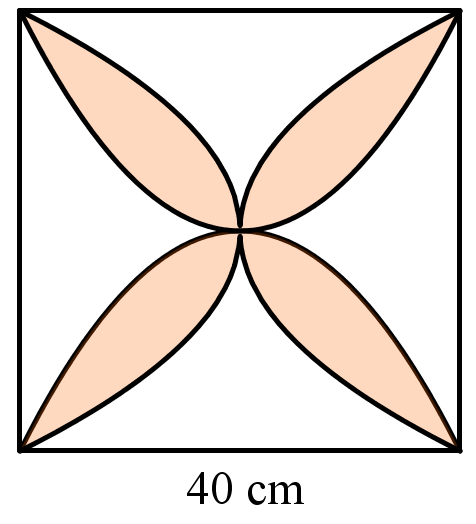
Chọn hệ tọa độ như hình vẽ (1 đơn vị trên trục bằng \(10\,{\rm{cm}} = 1\,{\rm{dm}}\)), các cánh hoa tạo bởi các đường parabol có phương trình \(y = \frac{{{x^2}}}{3}\), \(y =  - \frac{{{x^2}}}{3}\),\(x =  - \frac{{{y^2}}}{3}\),\(x = \frac{{{y^2}}}{3}\).

Diện tích một cánh hoa (nằm trong góc phần tư thứ nhất) bằng diện tích hình phẳng giới hạn bởi hai đồ thị hàm số\(y = \frac{{{x^2}}}{3}\),\(y = \sqrt {3x} \) và hai đường thẳng \(x = 0;x = 3\).

Do đó diện tích một cánh hoa bằng: \(\int\limits_0^3 {\left( {\sqrt {3x}  - \frac{{{x^2}}}{3}} \right){\rm{d}}x} \) \[ = 3\left( {{\rm{d}}{{\rm{m}}^{\rm{2}}}} \right) = 300\left( {{\rm{c}}{{\rm{m}}^{\rm{2}}}} \right)\].

Đáp án: 300.

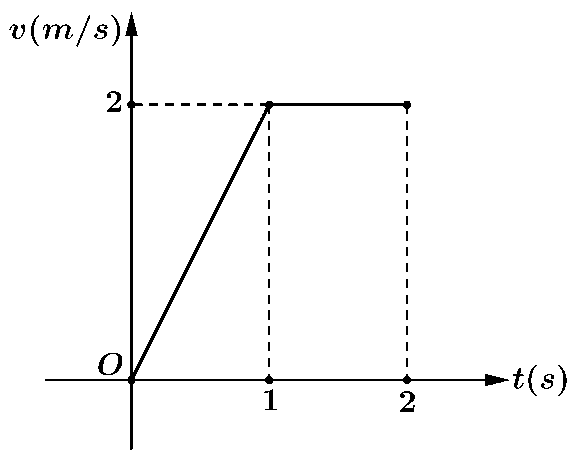
a) Sai. Dựa vào đồ thị \(v\left( t \right)\).

b) Đúng. Trong \(3\) giây đầu tiên, vận tốc của chuyển động là \(v\left( t \right) = 11\,\left( {{\rm{m/s}}} \right)\).

Do đó quãng đường chất điểm chuyển động trong \(3\)giây đầu tiên là: \({S_1} = \int\limits_0^3 {11{\rm{d}}t} \,\,\left( {\rm{m}} \right)\).

c) Đúng. Trong khoảng thời gian từ \(8\) đến \(15\) giây, đồ thị \(v\left( t \right)\) là một đường thẳng đi qua hai điểm \(\left( {8;21} \right)\) và \(\left( {15;0} \right)\). Ta có: \(v\left( t \right) = at + b\).

Từ giả thiết ta có hệ: \(\left\{ {\begin{array}{*{20}{c}}{8a + b = 21}\\{15a + b = 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{a =  - 3}\\{b = 45}\end{array}} \right.\).

Do đó \(v\left( t \right) =  - 3t + 45\,\,\left( {8 \le t \le 15} \right)\).

Quãng đường chất điểm đi được trong khoảng thời gian này là:

\({S_2} = \int\limits_8^{15} {\left( { - 3t + 45} \right){\rm{d}}t}  =  - \frac{{3{t^2}}}{2}\left| {\begin{array}{*{20}{c}}{15}\\8\end{array}} \right. + 45t\left| {\begin{array}{*{20}{c}}{15}\\8\end{array}} \right. = \frac{{147}}{2} = 73,5\,\left( {\rm{m}} \right)\).

d) Sai. Trong khoảng thời gian từ \(3\) đến \(8\) giây đồ thị \(v\left( t \right)\) là một Parabol đi qua các điểm có tọa độ lần lượt là  \(\left( {3;11} \right),\left( {5;3} \right),\left( {8;21} \right)\) có phương trình dạng: \(v\left( t \right) = a{t^2} + bt + c\).

Từ giả thiết ta có: \(\left\{ {\begin{array}{*{20}{c}}{9a + 3b + c = 11}\\{25a + 5b + c = 3}\\{64a + 8b + c = 21}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{a = 2}\\{b =  - 20}\\{c = 53}\end{array}} \right.\)

Do đó: \(v\left( t \right) = 2{t^2} - 20t + 53\,\,\left( {3 \le t \le 8} \right)\).

Quãng đường chất điểm đi được trong khoảng thời gian này là:

\[{S_3} = \int\limits_3^8 {v\left( t \right){\rm{d}}t}  = \int\limits_3^8 {\left( {2{t^2} - 20t + 53} \right){\rm{d}}t = \,\,} \left( {\frac{{2{t^3}}}{3} - 10{t^2} + 53t} \right)\left| {\begin{array}{*{20}{c}}8\\3\end{array}} \right. = \frac{{115}}{3}\,\,\,\left( {\rm{m}} \right)\].

Vận tốc trung bình của chất điểm trong khoảng thời gian này là: \({v_{tb}} = \frac{{{S_3}}}{5} = \frac{{23}}{3} \approx 7,67\,\left( {{\rm{m/s}}} \right)\).