Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = {e^x}\), trục hoành và hai đường thẳng \(x = 0\) và \(x = 3\).
Quảng cáo
Trả lời:
Chọn B
Diện tích hình phẳng cần tìm là \(S = \int\limits_0^3 {{e^x}dx} = \left. {{e^x}} \right|_0^3 = {e^3} - 1\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
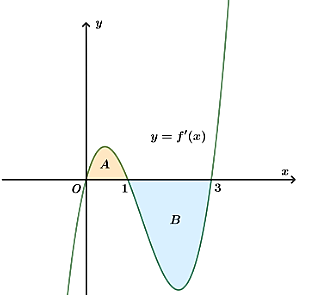
Ta có \(\int\limits_0^3 {f'\left( x \right)dx} = \int\limits_0^1 {f'\left( x \right)dx} + \int\limits_1^3 {f'\left( x \right)dx} = {S_A} - {S_B} = 4 - 10 = - 6\).
Lại có \(\int\limits_0^3 {f'\left( x \right)dx} = \left. {f\left( x \right)} \right|_0^3 = f\left( 3 \right) - f\left( 0 \right) = - 6 \Rightarrow f\left( 3 \right) = - 6 + f\left( 0 \right) = - 6 + 2 = - 4\).
Trả lời: −4.
Lời giải
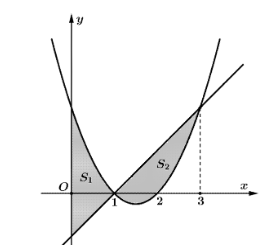
a) Phương trình hoành độ giao điểm: \({x^2} - 3x + 2 = x - 1 \Leftrightarrow {x^2} - 4x + 3 = 0\)\( \Leftrightarrow x = 1\) hoặc \(x = 3\).
Diện tích cần tính là \({S_2} = \int\limits_1^3 {\left| {x - 1 - \left( {{x^2} - 3x + 2} \right)} \right|dx} = \int\limits_1^3 {\left( { - {x^2} + 4x - 3} \right)dx} = \left. {\left( { - \frac{{{x^3}}}{3} + 2{x^2} - 3x} \right)} \right|_1^3 = \frac{4}{3}\).
b) \({S_1} = \int\limits_0^1 {\left| {{x^2} - 3x + 2 - \left( {x - 1} \right)} \right|dx} = \int\limits_0^1 {\left( {{x^2} - 4x + 3} \right)dx} \)\( = \left. {\frac{{{x^3}}}{3} - 2{x^2} + 3x} \right|_0^1 = \frac{4}{3}\).
c) \({S_1} = {S_2} = \frac{4}{3}\).
d) Diện tích cần tìm là \(S = \int\limits_0^3 {\left| {{x^2} - 3x + 2 - \left( {x - 1} \right)} \right|dx} = \int\limits_0^3 {\left| {{x^2} - 4x + 3} \right|dx} \)\( = \int\limits_0^1 {\left( {{x^2} - 4x + 3} \right)dx} + \int\limits_1^3 {\left( { - {x^2} + 4x - 3} \right)dx} = {S_1} + {S_2} = 2.\frac{4}{3} = \frac{8}{3}\).
Đáp án: a) Sai; b) Đúng; c) Đúng; d) Sai.
Câu 3
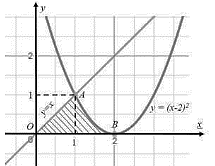
A. \(\frac{5}{6}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.