Cho tam giác ABC với trung tuyến AM và trọng tâm G. Tìm số thực k thỏa mãn \(\overrightarrow {GM} = k\overrightarrow {GA} \).
Quảng cáo
Trả lời:
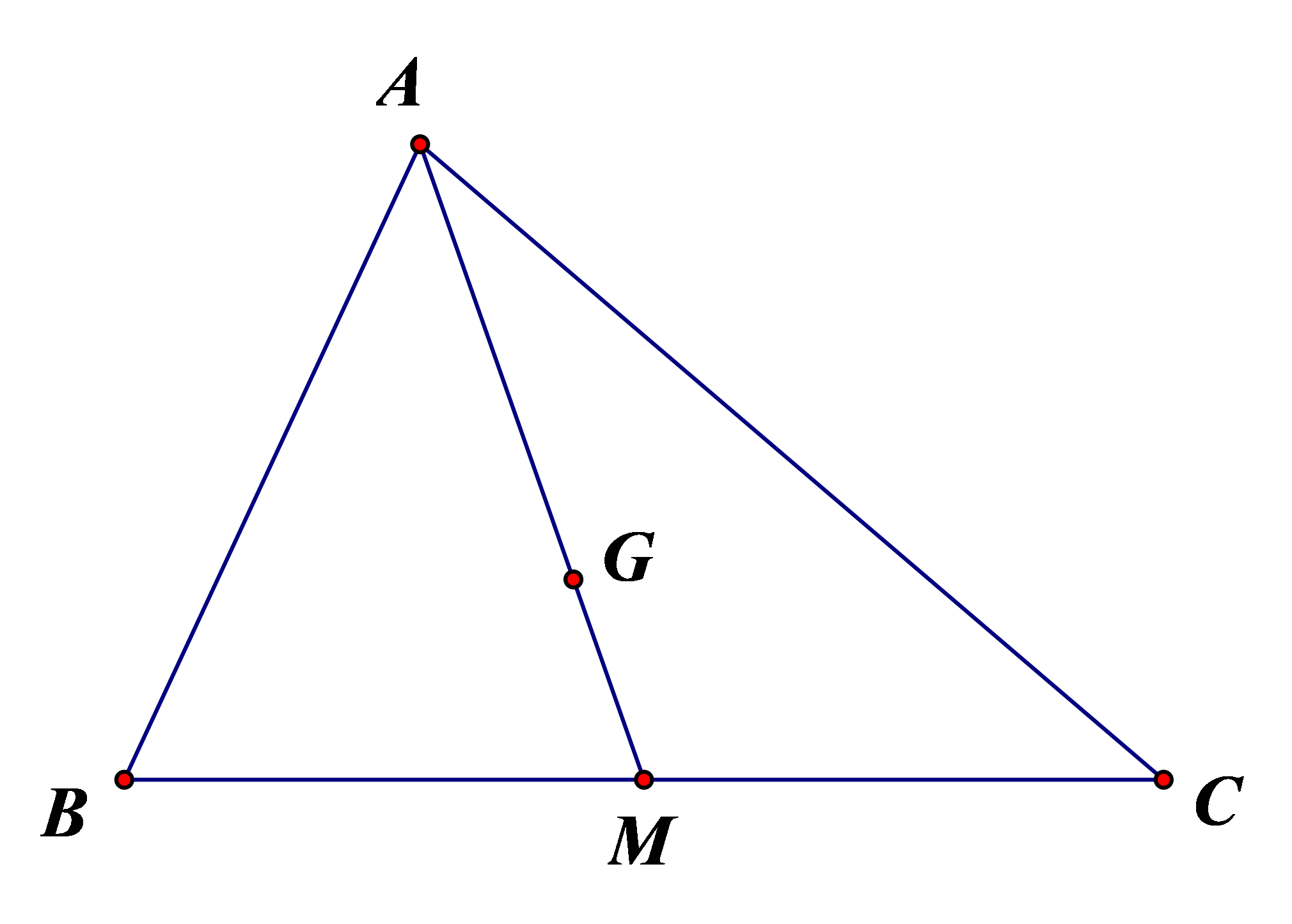
Ta có \(\overrightarrow {GM} = \frac{1}{3}\overrightarrow {AM} \)\( \Leftrightarrow \overrightarrow {GM} = \frac{1}{3}.\frac{3}{2}\overrightarrow {AG} \)\( \Leftrightarrow \overrightarrow {GM} = - \frac{1}{2}\overrightarrow {GA} \).
Trả lời: −0,5.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Lí, Hóa, Sinh 10 cho cả 3 bộ KNTT, CTST và CD VietJack - Sách 2025 ( 40.000₫ )
- Sách - Sổ tay kiến thức trọng tâm Vật lí 10 VietJack - Sách 2025 theo chương trình mới cho 2k9 ( 31.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
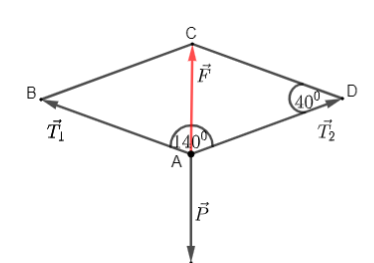
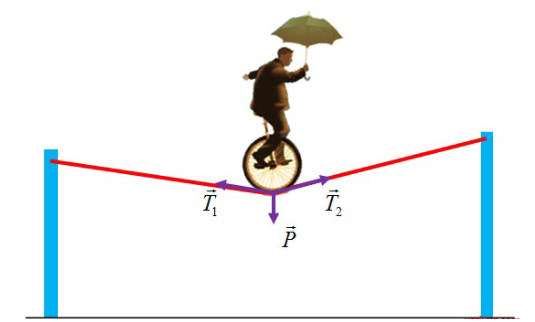
Theo quy tắc hình bình hành ta có \(\overrightarrow {{T_1}} + \overrightarrow {{T_2}} = \overrightarrow F \).
Khi diễn viên xiếc đạt trạng thái cân bằng trên dây, ta có \(\overrightarrow {{T_1}} + \overrightarrow {{T_2}} + \overrightarrow P = \overrightarrow 0 \)\( \Leftrightarrow \overrightarrow F = - \overrightarrow P \) và \(\left| {\overrightarrow F } \right| = \left| { - \overrightarrow P } \right| = 700\) (N).
Ta có góc tạo bởi \(\overrightarrow {{T_1}} \) và \(\overrightarrow {{T_2}} \) bằng 140° \( \Rightarrow \widehat {CDA} = 180^\circ - 140^\circ = 40^\circ \).
Dây không giãn nên \(\left| {\overrightarrow {{T_1}} } \right| = \left| {\overrightarrow {{T_2}} } \right|\).
Xét \(\Delta ADC\) có \({F^2} = T_1^2 + T_2^2 - 2{T_1}{T_2}\cos \widehat {CDA}\)\( \Leftrightarrow {F^2} = 2T_1^2\left( {1 - \cos 40^\circ } \right)\)
\( \Rightarrow {T_1} = \sqrt {\frac{{{F^2}}}{{2\left( {1 - \cos 40^\circ } \right)}}} = \sqrt {\frac{{{{700}^2}}}{{2\left( {1 - \cos 40^\circ } \right)}}} \approx 1023\) N.
Lời giải
Gọi \(x;y\)(chiếc) là số lượng bánh nướng, bánh dẻo mà xí nghiệp cần sản xuất (\(x,y \in \mathbb{N}\)).
Khối lượng bột mỳ cần dùng là \(0,12x + 0,16y\) (kg).
Khối lượng đường cần dùng là \(0,06x + 0,04y\) (kg).
Theo đề ta có hệ \(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\y \le 3x\\3x + 4y \le 15000\\3x + 2y \le 12000\end{array} \right.\).
Số tiền lãi thu được là \(T = 8x + 6y\) (nghìn đồng).
Bài toán trở thành tìm giá trị lớn nhất của \(T = 8x + 6y\) trên miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\y \le 3x\\3x + 4y \le 15000\\3x + 2y \le 12000\end{array} \right.\).
Miền nghiệm của hệ bất phương trình là miền tứ giác OABC kể cả cạnh (phần không gạch) với \(O\left( {0;0} \right),A\left( {4000;0} \right),B\left( {3000;1500} \right),C\left( {1000;3000} \right)\).
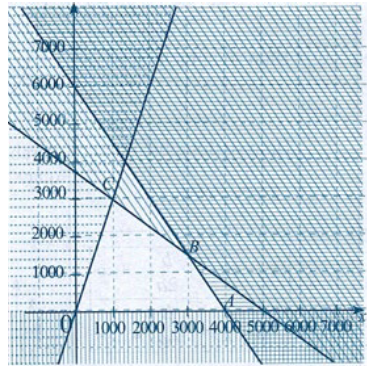
Với \(O\left( {0;0} \right)\) thì \(T = 0\).
Với \(A\left( {4000;0} \right)\) thì \(T = 32000\).
Với \(B\left( {3000;1500} \right)\) thì \(T = 33000\).
Với \(O\left( {1000;3000} \right)\) thì \(T = 26000\).
Do đó để đạt được tiền lãi cao nhất thì xí nghiệp nên sản xuất 3000 chiếc bánh nướng và 1500 chiếc bánh dẻo.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.