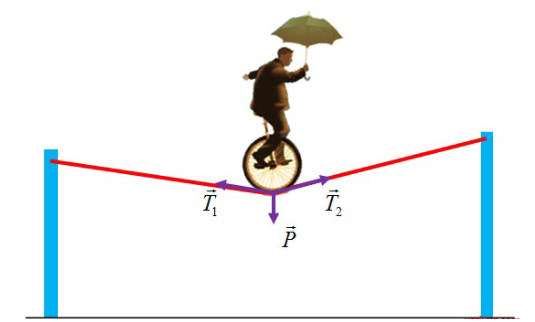
Khi một quả bóng được đá lên, nó sẽ đạt đến độ cao nào đó rồi rơi xuống. Hình vẽ bên dưới minh họa quỹ đạo của quả bóng là một phần của cung parabol trong mặt phẳng tọa độ Oth, trong đó \(t\) là thời gian (tính bằng giây) kể từ khi quả bóng được đá lên và \(h\) là độ cao (tính bằng mét) của quả bóng. Giả thiết rằng quả bóng được đá từ mặt đất. Sau khoảng 2 (s) quả bóng đó lên đến vị trí cao nhất là 8 m. Hỏi sau 3 giây thì quả bóng cách mặt đất bao nhiêu mét?
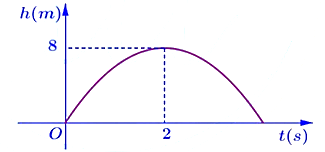
Khi một quả bóng được đá lên, nó sẽ đạt đến độ cao nào đó rồi rơi xuống. Hình vẽ bên dưới minh họa quỹ đạo của quả bóng là một phần của cung parabol trong mặt phẳng tọa độ Oth, trong đó \(t\) là thời gian (tính bằng giây) kể từ khi quả bóng được đá lên và \(h\) là độ cao (tính bằng mét) của quả bóng. Giả thiết rằng quả bóng được đá từ mặt đất. Sau khoảng 2 (s) quả bóng đó lên đến vị trí cao nhất là 8 m. Hỏi sau 3 giây thì quả bóng cách mặt đất bao nhiêu mét?

Quảng cáo
Trả lời:
Gọi hàm số bậc hai biểu thị độ cao h (m) theo thời gian t (s) là \(h = f\left( t \right) = a{t^2} + bt + c\left( {a < 0} \right)\).
Theo giả thiết, quả bóng được đá lên từ mặt đất, nghĩa là \(f\left( 0 \right) = c = 0\).
Do đó \(f\left( t \right) = a{t^2} + bt\).
Sau 2 giây quả bóng lên đến vị trí cao nhất là 8 m nên \(\left\{ \begin{array}{l} - \frac{b}{{2a}} = 2\\f\left( 2 \right) = 8\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}b = - 4a\\4a + 2b = 8\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}b = - 4a\\ - 4a = 8\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}a = - 2\\b = 8\end{array} \right.\).
Vậy \(f\left( t \right) = - 2{t^2} + 8t\).
Sau 3 giây quả bóng cách mặt đất một khoảng là \(h = f\left( 3 \right) = 6\) m.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Lí, Hóa, Sinh 10 cho cả 3 bộ KNTT, CTST và CD VietJack - Sách 2025 ( 40.000₫ )
- Sách - Sổ tay kiến thức trọng tâm Vật lí 10 VietJack - Sách 2025 theo chương trình mới cho 2k9 ( 31.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
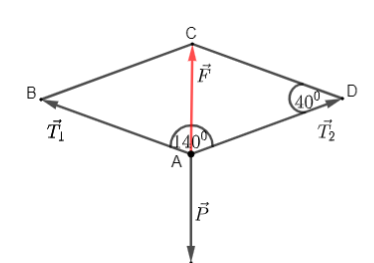
Theo quy tắc hình bình hành ta có \(\overrightarrow {{T_1}} + \overrightarrow {{T_2}} = \overrightarrow F \).
Khi diễn viên xiếc đạt trạng thái cân bằng trên dây, ta có \(\overrightarrow {{T_1}} + \overrightarrow {{T_2}} + \overrightarrow P = \overrightarrow 0 \)\( \Leftrightarrow \overrightarrow F = - \overrightarrow P \) và \(\left| {\overrightarrow F } \right| = \left| { - \overrightarrow P } \right| = 700\) (N).
Ta có góc tạo bởi \(\overrightarrow {{T_1}} \) và \(\overrightarrow {{T_2}} \) bằng 140° \( \Rightarrow \widehat {CDA} = 180^\circ - 140^\circ = 40^\circ \).
Dây không giãn nên \(\left| {\overrightarrow {{T_1}} } \right| = \left| {\overrightarrow {{T_2}} } \right|\).
Xét \(\Delta ADC\) có \({F^2} = T_1^2 + T_2^2 - 2{T_1}{T_2}\cos \widehat {CDA}\)\( \Leftrightarrow {F^2} = 2T_1^2\left( {1 - \cos 40^\circ } \right)\)
\( \Rightarrow {T_1} = \sqrt {\frac{{{F^2}}}{{2\left( {1 - \cos 40^\circ } \right)}}} = \sqrt {\frac{{{{700}^2}}}{{2\left( {1 - \cos 40^\circ } \right)}}} \approx 1023\) N.
Lời giải
Gọi \(x;y\)(chiếc) là số lượng bánh nướng, bánh dẻo mà xí nghiệp cần sản xuất (\(x,y \in \mathbb{N}\)).
Khối lượng bột mỳ cần dùng là \(0,12x + 0,16y\) (kg).
Khối lượng đường cần dùng là \(0,06x + 0,04y\) (kg).
Theo đề ta có hệ \(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\y \le 3x\\3x + 4y \le 15000\\3x + 2y \le 12000\end{array} \right.\).
Số tiền lãi thu được là \(T = 8x + 6y\) (nghìn đồng).
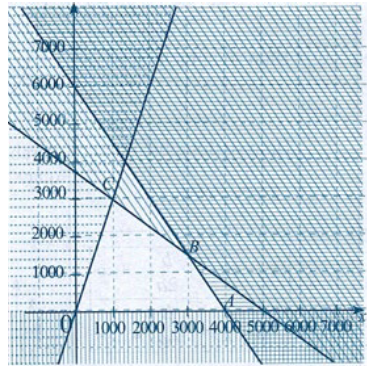
Bài toán trở thành tìm giá trị lớn nhất của \(T = 8x + 6y\) trên miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\y \le 3x\\3x + 4y \le 15000\\3x + 2y \le 12000\end{array} \right.\).
Miền nghiệm của hệ bất phương trình là miền tứ giác OABC kể cả cạnh (phần không gạch) với \(O\left( {0;0} \right),A\left( {4000;0} \right),B\left( {3000;1500} \right),C\left( {1000;3000} \right)\).
Với \(O\left( {0;0} \right)\) thì \(T = 0\).
Với \(A\left( {4000;0} \right)\) thì \(T = 32000\).
Với \(B\left( {3000;1500} \right)\) thì \(T = 33000\).
Với \(O\left( {1000;3000} \right)\) thì \(T = 26000\).
Do đó để đạt được tiền lãi cao nhất thì xí nghiệp nên sản xuất 3000 chiếc bánh nướng và 1500 chiếc bánh dẻo.
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.