Trong bóng đá, đá phạt đền là một hình thức đá phạt trực tiếp giữa 1 cầu thủ và 1 thủ môn. Bóng sẽ được đặt ở vị trí nằm trên đường trung trực của khung thành và cách khung thành \[11{\rm{ m}}.\] Biết chiều dài khung thành là \(7,23\,\;{\rm{m}}\). Góc sút \(\widehat {BAC}\) của cầu thủ khoảng
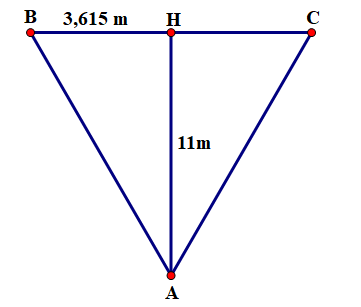
Trong bóng đá, đá phạt đền là một hình thức đá phạt trực tiếp giữa 1 cầu thủ và 1 thủ môn. Bóng sẽ được đặt ở vị trí nằm trên đường trung trực của khung thành và cách khung thành \[11{\rm{ m}}.\] Biết chiều dài khung thành là \(7,23\,\;{\rm{m}}\). Góc sút \(\widehat {BAC}\) của cầu thủ khoảng
Câu hỏi trong đề: Đề kiểm tra Toán 9 Cánh diều Chương 4 có đáp án !!
Quảng cáo
Trả lời:
Chọn B
Ta có \(BH = \frac{{BC}}{2} = 3,615\;\,({\rm{m)}}{\rm{.}}\)
Xét \(\Delta ACH\) vuông tại \[H,\] ta có:
\(\tan \widehat {HAB} = \frac{{BH}}{{AH}} = \frac{{3,615}}{{11}}\) nên \(\widehat {HAB} \approx 18^\circ \).
Suy ra \[\widehat {BAC} = 2\widehat {HAB} \approx 2 \cdot 18^\circ = 36^\circ .\]
Vậy góc sút của cầu thủ khoảng \(36^\circ \).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Lời giải
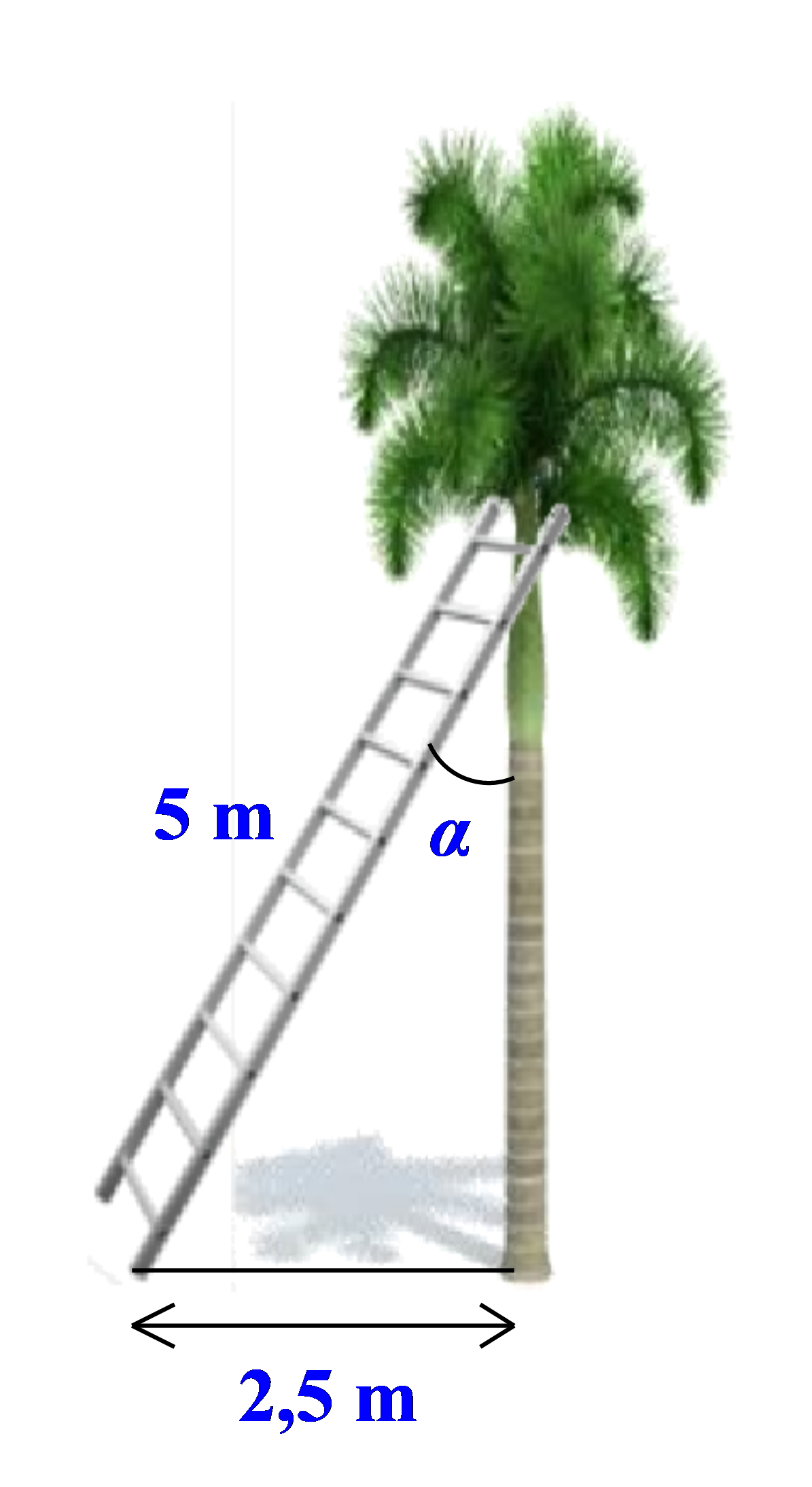
Xét \(\Delta ABH\) vuông tại \(A\), ta có:
\(\tan B = \frac{{AH}}{{AB}}\) hay \(\tan 63^\circ = \frac{{AH}}{{235}}\) nên \(AH = 235 \cdot \tan 63^\circ = 461\;\,({\rm{m)}}\).
Vậy chiều cao của tòa nhà này là \[461{\rm{ m}}.\]
Đáp án: 461.
Câu 2
Lời giải
Chọn C
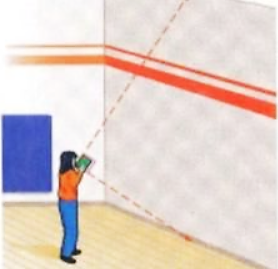
Gọi \(A,\,\,D\) là vị trí của người đứng;
\(C,\,\,D\) là vị trí bức tường phía trên và dưới cùng;
\[H\] là hình chiếu của \[A\] lên \[BC.\]
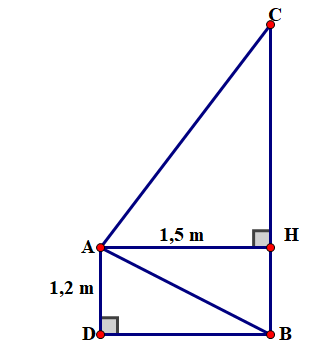
Tứ giác \[ADBH\] là hình chữ nhật nên \(BD = AH = 1,5\;\,{\rm{m}}\);
\[BH = AD = 1,2\;\,{\rm{m}}{\rm{.}}\]
Áp dụng định lí Pythagore vào tam giác \(ABD\) vuông tại \(D,\) ta có:
\(A{B^2} = A{D^2} + B{D^2} = 1,{2^2} + 1,{5^2} = 3,69\).
Suy ra \(AB = \sqrt {3,69} = 1,92\;\,({\rm{m}}).\)
Xét \(\Delta ABC\) vuông tại \[A,\] đường cao \[AH,\] ta có:
\(A{B^2} = BH \cdot BC\) hay \(BC = \frac{{A{B^2}}}{{BH}} = \frac{{3,69}}{{1,2}} \approx 3\;\,\,({\rm{m}})\).
Vậy chiều cao của bức tường là \[3{\rm{ m}}.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
![Lời giải Xét \(\Delta ABH\) vuông tại \(A\), ta có: \(\tan B = \frac{{AH}}{{AB}}\) hay \(\tan 63^\circ = \frac{{AH}}{{235}}\) nên \(AH = 235 \cdot \tan 63^\circ = 461\;\,({\rm{m)}}\). Vậy chiều cao của tòa nhà này là \[461{\rm{ m}}.\] Đáp án: 461. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/67-1761202758.png)
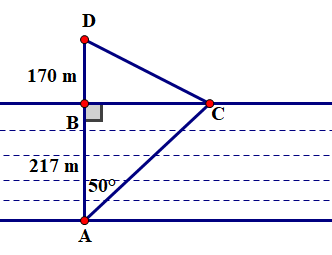
![Để xác định khoảng cách từ một gốc cây \[A\] trên một hòn đảo nh (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/43-1761183381.png)