Đường thẳng d: 2x - y = 2 chia mặt phẳng tọa độ thành hai miền I, II có bờ là đường thẳng d (như hình vẽ bên). Xác định miền nghiệm của bất phương trình 2.x - y 2.
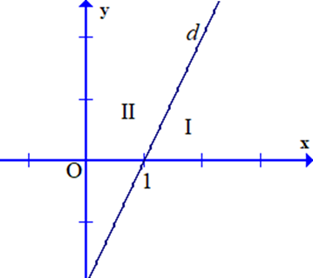
A. Nửa mặt phẳng I kể cả bờ d.
B. Nửa mặt phẳng II bỏ đi đường thẳng d.
Câu hỏi trong đề: Bộ 10 đề thi giữa kì 1 Toán 10 có đáp án !!
Quảng cáo
Trả lời:
Chọn A
Thay tọa độ điểm O (0;0) vào bất phương trình đã cho, ta có 2.0 - 0 2 là mệnh đề sai. Do vậy miền nghiệm của bất phương trình đã cho là miền I không chứa điểm O, kể cả bờ d.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Lí, Hóa, Sinh 10 cho cả 3 bộ KNTT, CTST và CD VietJack - Sách 2025 ( 40.000₫ )
- Sách - Sổ tay kiến thức trọng tâm Vật lí 10 VietJack - Sách 2025 theo chương trình mới cho 2k9 ( 31.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
Chọn C
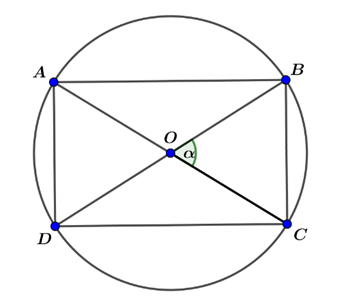
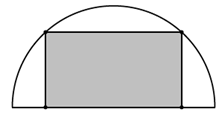
Xét đường tròn bán kính \[1\], ta cắt trên đó một hình chữ nhật \[ABCD\].
Khi đó \[{S_{ABCD}} = \frac{1}{2}AC.BD.\sin \alpha \]\[ = 2\sin \alpha \le 2\].
Dấu bằng xảy ra khi và chỉ khi \[\alpha = 90^\circ \].
Vậy diện tích lớn nhất của miếng tôn cắt trên nửa đường tròn bằng \[1\].
Lời giải
Gọi \(x,y\left( {x \ge 0,y \ge 0} \right)\) lần lượt là số ha đất trồng rau và hoa.
Diện tích đất trồng canh tác không vượt quá \(8\) ha nên ta có \(x + y \le 8\).
Số ngày công sử dụng không vượt quá \(180\) ngày nên \(2x + 3y \le 180\).
Từ đó, ta có hệ bất phương trình \(\left\{ {\begin{array}{*{20}{l}}{x + y \le 8}\\{2x + 3y \le 180}\\{x \ge 0}\\{y \ge 0.}\end{array}} \right.\)
Ta cần tìm \(x,y\) sao cho \(T\left( {x,y} \right) = 3x + 4y\) lớn nhất.
Miền nghiệm của hệ được biểu diễn như sau:
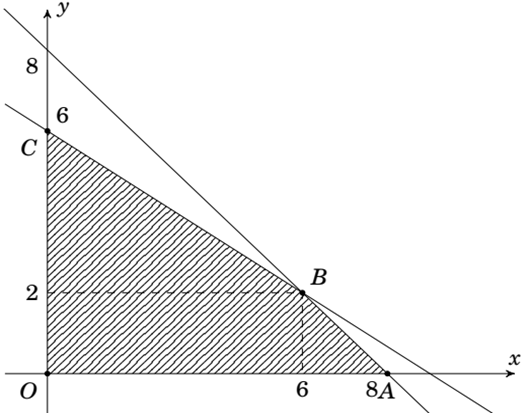
Miền nghiệm của hệ bất phương trình trên là miền trong của tứ giác \(OABC\), kể cả các cạnh của tứ giác đó, với \(O\left( {0;0} \right)\), \(A\left( {8;0} \right)\), \(B\left( {6;2} \right)\), \(C\left( {0;6} \right)\).
Tại \(O\left( {0;0} \right)\), ta có \(T = 3 \cdot 0 + 4 \cdot 0 = 0\).
Tại \(A\left( {8;0} \right)\), ta có \(T = 3 \cdot 8 + 4 \cdot 0 = 24\).
Tại \(B\left( {6;2} \right)\), ta có \(T = 3 \cdot 6 + 4 \cdot 2 = 26\).
Tại \(C\left( {0;6} \right)\), ta có \(T = 3 \cdot 0 + 4 \cdot 6 = 24\).
Vậy số lợi nhuận cao nhất mà gia đình chị Minh thu được từ trồng rau và hoa là \(26\) triệu đồng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. Không tồn tại giá trị nhỏ nhất của \(F\).
B. \(\min F = 2\,khi\,x = 0,\,\,y = 2\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \(\frac{1}{2}\).
B. \(\frac{{\sqrt 2 - 2\sqrt 3 }}{2}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.