Bạn Nam tiết kiệm được 450 nghìn đồng. Trong đợt ủng hộ các bạn học sinh đồng bào miền Trung bị lũ lụt vừa qua, bạn Nam đã ủng hộ \(x\) tờ tiền loại 20 nghìn đồng, \(y\)tờ tiền loại 10 nghìn đồng. Khi đó bất phương trình biểu diễn tổng số tiền mà bạn Nam đã ủng hộ có dạng \(ax + by \le c\). Tính giá trị của biểu thức \(P = c - 2a - b\).
Bạn Nam tiết kiệm được 450 nghìn đồng. Trong đợt ủng hộ các bạn học sinh đồng bào miền Trung bị lũ lụt vừa qua, bạn Nam đã ủng hộ \(x\) tờ tiền loại 20 nghìn đồng, \(y\)tờ tiền loại 10 nghìn đồng. Khi đó bất phương trình biểu diễn tổng số tiền mà bạn Nam đã ủng hộ có dạng \(ax + by \le c\). Tính giá trị của biểu thức \(P = c - 2a - b\).
Quảng cáo
Trả lời:
Trả lời: 400
Số tiền 20 nghìn đồng bạn Nam đã ủng hộ là: \(20x\) (nghìn đồng).
Số tiền 10 nghìn đồng bạn Nam đã ủng hộ là: \(10y\) (nghìn đồng).
Theo đề ta có: \(20x + 10y \le 450\).
Suy ra \(a = 20;b = 10;c = 450\). Do đó \(P = 450 - 2.20 - 10 = 400\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Lí, Hóa, Sinh 10 cho cả 3 bộ KNTT, CTST và CD VietJack - Sách 2025 ( 40.000₫ )
- Trọng tâm Toán, Văn, Anh 10 cho cả 3 bộ KNTT, CTST, CD VietJack - Sách 2025 ( 13.600₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Trả lời: 3.
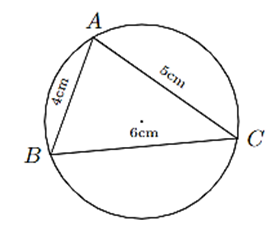
Áp dụng định lí côsin cho tam giác ABC, ta có: \(\cos A = \frac{{A{B^2} + A{C^2} - B{C^2}}}{{2.AB.AC}} = \frac{{{4^2} + {5^2} - {6^2}}}{{2.4.5}} = \frac{1}{8}\).
Mà \(\widehat {\rm{A}} < 180^\circ \) nên \(\sin A = \sqrt {1 - {{\cos }^2}A} = \sqrt {1 - \frac{1}{{64}}} = \frac{{3\sqrt 7 }}{8}\).
Áp dụng định lí sin, ta có \(\frac{{BC}}{{\sin A}} = 2R \Rightarrow R = \frac{{BC}}{{2\sin A}} = \frac{6}{{2.\frac{{3\sqrt 7 }}{8}}} \approx 3\)(cm).
Lời giải
a) Đ, b) S, c) Đ, d) Đ
a) \(B{C^2} = A{B^2} + A{C^2} - 2.AB.AC.\cos \widehat {\rm{A}}\).
b) Ta có \(\cos \widehat B = \frac{{A{B^2} + B{C^2} - A{C^2}}}{{2.AB.BC}} = \frac{{{{\left( {1 + \sqrt 3 } \right)}^2} + 6 - 4}}{{2.\left( {1 + \sqrt 3 } \right).\sqrt 6 }} = \frac{{\sqrt 2 }}{2} \Rightarrow \widehat B = 45^\circ \).
c) Ta có \(S = \frac{1}{2}.AB.BC.\sin \widehat B = \frac{1}{2}.\left( {1 + \sqrt 3 } \right).\sqrt 6 .\sin 45^\circ = \frac{{3 + \sqrt 3 }}{2}\).
d) Vì \(\frac{{AC}}{{\sin B}} = 2R \Rightarrow R = \frac{{AC}}{{2\sin B}} = \frac{2}{{2.\sin 45^\circ }} = \sqrt 2 \).
Câu 3
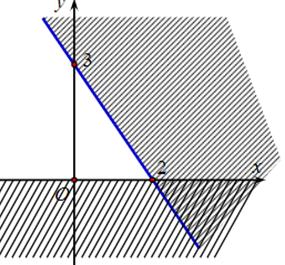
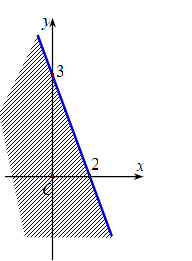
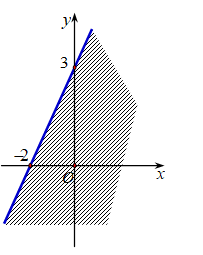
A. \[\left\{ \begin{array}{l}y \ge 0\\3x + 2y < - 6\end{array} \right.\].
B. \[\left\{ \begin{array}{l}x > 0\\3x + 2y < 6\end{array} \right.\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.