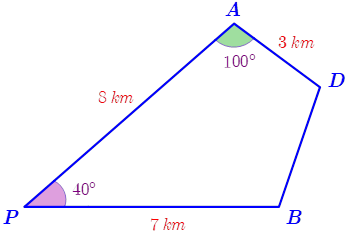
Hai bạn An và Hưng cùng xuất phát từ điểm \(P\), đi theo hai hướng khác nhau và tạo với nhau một góc \(40^\circ \) để đến đích là điểm \(D\). Biết rằng họ dừng lại để ăn trưa lần lượt tại \(A\) và \(B\) (như hình vẽ minh hoạ). Hỏi Hưng phải đi bao xa nữa để đến được đích (làm tròn kết quả đến hàng phần mười)?

Quảng cáo
Trả lời:
Trả lời: 3,5
Xét tam giác \(APB\) có \(A{B^2} = A{P^2} + P{B^2} - 2.AP.PB.\cos \widehat {APB}\)\( = {8^2} + {7^2} - 2.8.7.\cos 40^\circ \approx 27,2\). Suy ra \(AB \approx 5,22\).
Có \(\cos \widehat {PAB} = \frac{{P{A^2} + A{B^2} - P{B^2}}}{{2.PA.BA}} = \frac{{{8^2} + {{5,22}^2} - {7^2}}}{{2.8.5,22}} \approx 0,51\).
Suy ra \(\widehat {PAB} \approx 60^\circ \) \( \Rightarrow \widehat {BAD} \approx 100^\circ - 60^\circ = 40^\circ \).
Xét \(\Delta ABD\) có \(B{D^2} = A{D^2} + B{A^2} - 2.DA.BA.\cos \widehat {DAB}\)\( = {3^2} + {5,22^2} - 2.3.5,22.\cos 40^\circ \approx 12,26\).
Suy ra \(DB \approx 3,5\) (km).
Vậy Hưng phải đi khoảng 3,5 km nữa để đến được đích.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Toán, Văn, Anh 10 cho cả 3 bộ KNTT, CTST, CD VietJack - Sách 2025 ( 13.600₫ )
- Sách - Sổ tay kiến thức trọng tâm Vật lí 10 VietJack - Sách 2025 theo chương trình mới cho 2k9 ( 31.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. \(\overrightarrow {AB} = 2\overrightarrow {DC} \).
B. \(\overrightarrow {CA} + \overrightarrow {CB} = 2\overrightarrow {CE} \).
Lời giải
Đáp án đúng là: D
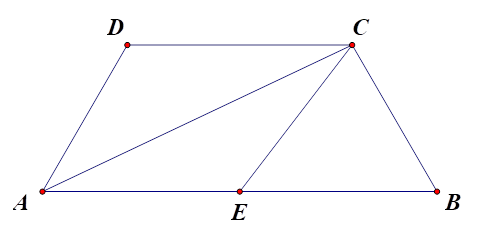
Vì \(AB = 2CD\) nên \(\overrightarrow {AB} = 2\overrightarrow {DC} \).
Vì E là trung điểm của AB nên \(\overrightarrow {CA} + \overrightarrow {CB} = 2\overrightarrow {CE} \).
Vì ADCE là hình bình hành nên \(\overrightarrow {AD} = \overrightarrow {EC} \).
Vì DCBE là hình bình hành nên \(\overrightarrow {DE} = \overrightarrow {CB} \).
Câu 2
A. \(\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \).
B. \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \).
Lời giải
Đáp án đúng là: D
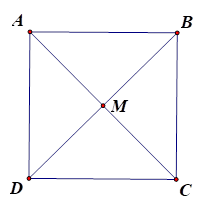
\(\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \) (quy tắc ba điểm).
\(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \) (quy tắc hình bình hành).
\(\overrightarrow {BA} + \overrightarrow {BC} = \overrightarrow {BD} = 2\overrightarrow {BM} \) (vì M là trung điểm của \(BD\)).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. Hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) được gọi là bằng nhau nếu chúng cùng phương.
B. Hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) được gọi là bằng nhau nếu chúng ngược hướng và cùng độ dài.
C. Hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) được gọi là bằng nhau nếu chúng cùng độ dài.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \(\frac{{\sqrt 3 }}{3}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.