(1,0 điểm) Để trang trí cho quán trà sữa sắp mở cửa của mình, bạn Việt quyết định tô màu một mảng tường hình vuông cạnh bằng 1 m. Phần tô màu dự kiến là các hình vuông nhỏ được đánh số lần lượt là \(1;\,\,2;\,...;\,n,\) trong đó cạnh của hình vuông kế tiếp bằng một nửa cạnh hình vuông trước đó. Giả sử quá trình tô màu của Việt có thể diễn ra nhiều giờ. Hỏi bạn Việt tô màu đến hình vuông thứ mấy thì diện tích của hình vuông được tô bắt đầu nhỏ hơn \(\frac{1}{{1\,\,000}}\,\,{{\rm{m}}^{\rm{2}}}?\)
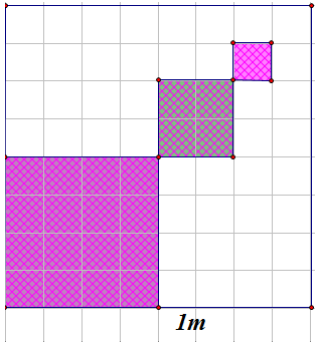
(1,0 điểm) Để trang trí cho quán trà sữa sắp mở cửa của mình, bạn Việt quyết định tô màu một mảng tường hình vuông cạnh bằng 1 m. Phần tô màu dự kiến là các hình vuông nhỏ được đánh số lần lượt là \(1;\,\,2;\,...;\,n,\) trong đó cạnh của hình vuông kế tiếp bằng một nửa cạnh hình vuông trước đó. Giả sử quá trình tô màu của Việt có thể diễn ra nhiều giờ. Hỏi bạn Việt tô màu đến hình vuông thứ mấy thì diện tích của hình vuông được tô bắt đầu nhỏ hơn \(\frac{1}{{1\,\,000}}\,\,{{\rm{m}}^{\rm{2}}}?\)

Quảng cáo
Trả lời:
Diện tích của hình vuông lập thành cấp số nhân với số hạng đầu tiên là \({u_1} = \frac{1}{4};\,\,q = \frac{1}{4}.\)
Do đó số hạng tổng quát của là \({u_n} = \frac{1}{4} \cdot {\left( {\frac{1}{4}} \right)^{n\, - \,1}} = \frac{1}{{{4^n}}}\,\,\left( {n \ge 1} \right)\).
Để tính diện tích của hình vuông tô màu nhỏ hơn \(\frac{1}{{1\,\,000}}\,\,{{\rm{m}}^{\rm{2}}}\).
Khi đó \(\frac{1}{{{4^n}}} < \frac{1}{{1\,\,000}}\, \Leftrightarrow {4^n} > 1\,\,000 \Rightarrow n \ge 5.\)
Vậy tô màu từ hình vuông thứ 5 thỏa mãn yêu cầu bài toán.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Sách - Sổ tay kiến thức trọng tâm Vật lí 10 VietJack - Sách 2025 theo chương trình mới cho 2k9 ( 31.000₫ )
- Trọng tâm Lí, Hóa, Sinh 10 cho cả 3 bộ KNTT, CTST và CD VietJack - Sách 2025 ( 40.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
![Cho tam giác \[ABC\] có trực tâm \(H\). (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/11/7-1763354073.png)
Do \(M\) là trung điểm của cạnh \(BC\) nên ta có:
\[\overrightarrow {MH} \cdot \overrightarrow {MA} = \frac{1}{2}\left( {\overrightarrow {BH} + \overrightarrow {CH} } \right) \cdot \frac{1}{2}\left( {\overrightarrow {BA} + \overrightarrow {CA} } \right)\] \[ = \frac{1}{4}\left( {\overrightarrow {BH} \cdot \overrightarrow {BA} + \overrightarrow {BH} \cdot \overrightarrow {CA} + \overrightarrow {CH} \cdot \overrightarrow {BA} + \overrightarrow {CH} \cdot \overrightarrow {CA} } \right)\]
Vì \(H\) là trực tâm của \[\Delta ABC,\] nên \[BH \bot CA{\rm{ }},{\rm{ }}CH \bot BA\] \[ \Rightarrow \overrightarrow {BH} \cdot \overrightarrow {CA} = 0,{\rm{ }}\overrightarrow {CH} \cdot \overrightarrow {BA} = 0\].
Do đó, \[\overrightarrow {MH} \cdot \overrightarrow {MA} = \frac{1}{4}\left( {\overrightarrow {BH} \cdot \overrightarrow {BA} + \overrightarrow {CH} \cdot \overrightarrow {CA} } \right)\]
\[ = \frac{1}{4}\left[ {\overrightarrow {BH} \cdot \left( {\overrightarrow {BC} + \overrightarrow {CA} } \right) + \overrightarrow {CH} \cdot \left( {\overrightarrow {BA} - \overrightarrow {BC} } \right)} \right] = \frac{1}{4}\left( {\overrightarrow {BH} \cdot \overrightarrow {BC} - \overrightarrow {CH} \cdot \overrightarrow {BC} } \right)\]
\( = \frac{1}{4} \cdot \overrightarrow {BC} \cdot \left( {\overrightarrow {BH} - \overrightarrow {CH} } \right) = \frac{1}{4} \cdot \overrightarrow {BC} \cdot \left( {\overrightarrow {BH} + \overrightarrow {HC} } \right) = \frac{1}{4} \cdot \overrightarrow {BC} \cdot \overrightarrow {BC} = \frac{1}{4}{\overrightarrow {BC} ^2} = \frac{1}{4}B{C^2}\).
Vậy \[\overrightarrow {MH} \cdot \overrightarrow {MA} = \frac{1}{4}B{C^2}\].
Câu 2
Lời giải
Đáp án đúng là: A
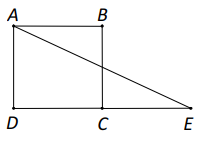
Vì \(E\) là điểm đối xứng của \(D\) qua \(C\) nên \(C\) là trung điểm của \(DE\), do đó \(DE = 2DC = 2 \cdot 3 = 6\).
Ta có: \(\overrightarrow {AE} \cdot \overrightarrow {AB} = \left( {\overrightarrow {AD} + \overrightarrow {DE} } \right) \cdot \overrightarrow {AB} = \overrightarrow {AD} \cdot \overrightarrow {AB} + \overrightarrow {DE} \cdot \overrightarrow {AB} \)
Do \(AB \bot AD\) nên \(\overrightarrow {AD} \cdot \overrightarrow {AB} = 0\).
Hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {DE} \) cùng hướng nên \(\cos \left( {\overrightarrow {AB} ,\,\,\overrightarrow {DE} } \right) = 0^\circ \).
Do đó, \(\overrightarrow {DE} \cdot \overrightarrow {AB} = \left| {\overrightarrow {DE} } \right| \cdot \left| {\overrightarrow {AB} } \right| \cdot \cos \left( {\overrightarrow {AB} ,\,\overrightarrow {DE} } \right) = DE \cdot AB \cdot \cos 0^\circ = 6 \cdot 3 \cdot 1 = 18\).
Vậy \(\overrightarrow {AE} \cdot \overrightarrow {AB} = 0 + 18 = 18\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.