Mẫu số liệu dưới đây thống kê thời gian chờ xe bus (đơn vị: phút) của 10 học sinh ở cùng một bến: 1, 4, 5, 6, 6, 8, 10, 11, 12, 25.
Thời gian chờ xe bus trung bình của 10 học sinh trên là.
A. \(8,8\) phút.
Quảng cáo
Trả lời:
Đáp án đúng là: A
Thời gian chờ xe bus trung bình của 10 học sinh là
\(\overline x = \frac{{1 + 4 + 5 + 6 + 6 + 8 + 10 + 11 + 12 + 25}}{{10}} = 8,8\) phút.
Câu hỏi cùng đoạn
Câu 2:
Mốt của mẫu số liệu trên là
A. \(25\).
Đáp án đúng là: B
Mốt của mẫu số liệu là 6.
Câu 3:
Giá trị ngoại lệ của mẫu số liệu trên là
A. \(25\).
Đáp án đúng là: A
Ta có \({Q_1} = 5;{Q_3} = 11\).
Suy ra \({\Delta _Q} = {Q_3} - {Q_1} = 6\).
Mà \({Q_1} - 1,5{\Delta _Q} = - 4;{Q_3} + 1,5{\Delta _Q} = 20\).
Giá trị ngoại lệ của mẫu số liệu trên là 25.
Câu 4:
Độ lệch chuẩn về thời gian chờ xe bus của 10 học sinh trên là (làm tròn kết quả đến hàng phần trăm).
A. \(6,07\) phút.
Đáp án đúng là: B
Ta có
\({s^2} = \frac{{{{\left( {1 - 8,8} \right)}^2} + {{\left( {4 - 8,8} \right)}^2} + {{\left( {5 - 8,8} \right)}^2} + 2{{\left( {6 - 8,8} \right)}^2} + {{\left( {8 - 8,8} \right)}^2} + {{\left( {10 - 8,8} \right)}^2}}}{{10}}\)
\( + \frac{{{{\left( {11 - 8,8} \right)}^2} + {{\left( {12 - 8,8} \right)}^2} + {{\left( {25 - 8,8} \right)}^2}}}{{10}} = 39,36\).
Suy ra \(s = \sqrt {39,36} \approx 6,27\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Toán, Văn, Anh 10 cho cả 3 bộ KNTT, CTST, CD VietJack - Sách 2025 ( 13.600₫ )
- Sách - Sổ tay kiến thức trọng tâm Vật lí 10 VietJack - Sách 2025 theo chương trình mới cho 2k9 ( 31.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Đ, b) Đ, c) Đ, d) S
\(y = - {x^2} + 2x - 5;(a = - 1,b = 2,c = - 5)\).
a) Tập xác định: \(D = \mathbb{R}\).
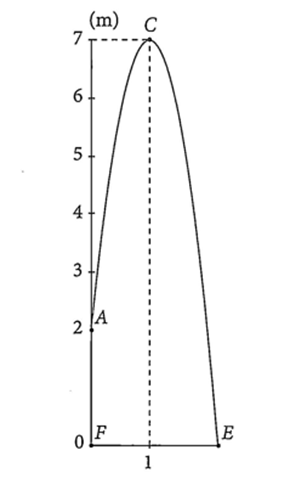
b) Tọa độ đỉnh \(I\) của parabol:
\({x_I} = - \frac{b}{{2a}} = 1,{y_I} = - {1^2} + 2.1 - 5 = - 4\) hay \(I(1; - 4)\).
c) Định hướng cho bảng biến thiên: Do \(a = - 1 < 0\) nên bề lõm parabol hướng xuống.
Bảng biến thiên:
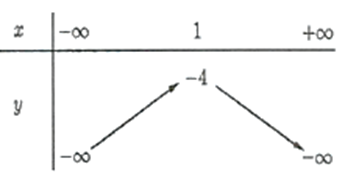
Kết luận:
- Hàm số đã cho đồng biến trên khoảng \(\left( { - \infty ;1} \right)\) và nghịch biến trên khoảng \(\left( {1; + \infty } \right)\).
- Giá trị lớn nhất của hàm số là \({y_{\max }} = - 4\), khi \(x = 1\). (Hàm số không có giá trị nhỏ nhất).
Lời giải
Trả lời: 4500
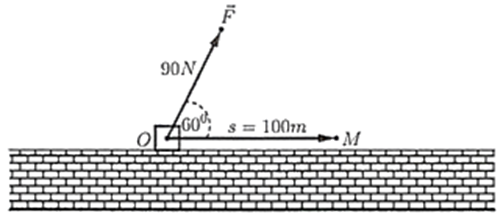
Đặt \(OM = s\) là đoạn đường mà vật di chuyển được với \(O\) là điểm đặt vật ban đầu. Công sinh ra bởi lực \(\vec F\) là:
\(A = \vec F \cdot \overrightarrow {OM} = |\vec F| \cdot |\overrightarrow {OM} | \cdot \cos (\vec F,\overrightarrow {OM} ) = 90 \cdot 100 \cdot \cos 60^\circ = 4500\;J{\rm{. }}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.