(1 điểm) Bạn Nam dùng đồng hồ bấm giờ để đo thời gian một vật rơi tự do (đơn vị: giây) từ tầng năm của một tòa nhà xuống mặt đất trong 10 lần cho kết quả như sau:
0,899; 0,898; 0,895; 0,901; 0,898; 0,902; 0,910; 0,312; 0,905; 0,899.
Nam nghĩa rằng giá trị 0,312 ở lần đo thứ 8 không chính xác. Hãy kiểm tra nghi ngờ của Nam.
(1 điểm) Bạn Nam dùng đồng hồ bấm giờ để đo thời gian một vật rơi tự do (đơn vị: giây) từ tầng năm của một tòa nhà xuống mặt đất trong 10 lần cho kết quả như sau:
0,899; 0,898; 0,895; 0,901; 0,898; 0,902; 0,910; 0,312; 0,905; 0,899.
Nam nghĩa rằng giá trị 0,312 ở lần đo thứ 8 không chính xác. Hãy kiểm tra nghi ngờ của Nam.
Câu hỏi trong đề: Bộ 10 đề thi cuối kì 1 Toán 10 Kết nối tri thức có đáp án !!
Quảng cáo
Trả lời:
Nhận thấy giá trị 0,312 nhỏ hơn rất nhiều so với các giá trị khác trong mẫu số liệu đã cho, do đó để kiểm tra nghi ngờ của Nam, ta cần xác định xem 0,312 có phải giá trị bất thường của mẫu số liệu hay không.
Sắp xếp mẫu số liệu đã cho theo thứ tự không giảm ta được:
0,312; 0,895; 0,898; 0,898; 0,899; 0,899; 0,901; 0,902; 0,905; 0,910.
Vì mẫu số liệu có 10 số liệu nên trung vị hay tứ phân vị thứ hai là trung bình cộng của số ở vị trí thứ năm và thứ sáu, do đó \({Q_2} = \frac{{0,899 + 0,899}}{2} = 0,899\).
Tứ phân vị thứ nhất là trung vị của mẫu 0,213; 0,895; 0,898; 0,898; 0,899.
Do đó, \({Q_1} = 0,898\).
Tứ phân vị thứ ba là trung vị của mẫu 0,899; 0,901; 0,902; 0,905; 0,910.
Do đó, \({Q_3} = 0,902\).
Khoảng tứ phân vị của mẫu số liệu là \({\Delta _Q} = {Q_3} - {Q_1} = 0,902 - 0,898 = 0,004\).
Ta có: \({Q_1} - 1,5{\Delta _Q} = 0,898 - 1,5 \cdot 0,004 = 0,892\).
Vì 0,312 < 0,892 nên 0,312 là giá trị bất thường của mẫu số liệu. Do đó, giá trị ở lần đó thứ 8 trong thí nghiệm trên không chính xác hay nghi ngờ của Nam là đúng.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Sách - Sổ tay kiến thức trọng tâm Vật lí 10 VietJack - Sách 2025 theo chương trình mới cho 2k9 ( 31.000₫ )
- Trọng tâm Lí, Hóa, Sinh 10 cho cả 3 bộ KNTT, CTST và CD VietJack - Sách 2025 ( 40.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
Đáp án đúng là: A
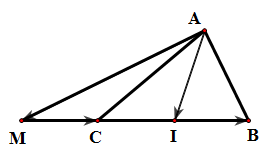
Gọi \(I\) là trung điểm của \(BC\). Khi đó \(C\) là trung điểm của \(MI\). Ta có:
\[\overrightarrow {AM} + \overrightarrow {AI} = 2\overrightarrow {AC} \Leftrightarrow \overrightarrow {AM} = - \overrightarrow {AI} + 2\overrightarrow {AC} = - \frac{1}{2}(\overrightarrow {AB} + \overrightarrow {AC} ) + 2\overrightarrow {AC} = - \frac{1}{2}\overrightarrow {AB} + \frac{3}{2}\overrightarrow {AC} \].
Câu 2
Lời giải
Đáp án đúng là: D
Vì \(\overrightarrow a \) và \(\overrightarrow b \) là hai vectơ ngược hướng và đều khác vectơ \(\overrightarrow 0 \) nên \(\left( {\overrightarrow a ,\,\,\overrightarrow b } \right) = 180^\circ \).
Do đó, \(\overrightarrow a \cdot \overrightarrow b = \left| {\overrightarrow a } \right| \cdot \left| {\overrightarrow b } \right| \cdot \cos \left( {\overrightarrow a ,\,\overrightarrow b } \right) = \left| {\overrightarrow a } \right| \cdot \left| {\overrightarrow b } \right| \cdot \cos 180^\circ = - \left| {\overrightarrow a } \right| \cdot \left| {\overrightarrow b } \right|\).
Câu 3
Người ta dự định dùng hai nguyên liệu là mía và củ cải đường để chiết xuất ít nhất 140 kg đường kính và 9 kg đường cát. Từ mỗi tấn mía có thể chiết xuất được 20 kg đường kính và 0,6 kg đường cát. Từ mỗi tấn củ cải đường có thể chiết xuất được 10 kg đường kính và 1,5 kg đường cát. Gọi số tấn mía cần dùng là \(x\) và số tấn củ cải đường cần dùng là \(y\). Biết rằng cơ sở cung cấp nguyên liệu chỉ có thể cung cấp không quá 10 tấn mía và không quá 9 tấn củ cải đường. Một hệ điều kiện giữa \(x\) và \(y\) thỏa mãn yêu cầu bài toán là
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.