(1 điểm) Kiểm tra khối lượng một số quả cam Vinh của hai lô hàng loại 1 và loại 2 được kết quả như sau (đơn vị: gam)
Loại 1
250
230
260
265
250
250
245
260
280
260
Lọai 2
200
180
210
220
185
210
215
190
195
190
a) Hãy tìm khoảng biến thiên, khoảng tứ phân vị, độ lệch chuẩn của khối lượng cam Vinh ở mỗi loại.
b) Khối lượng cam Vinh ở lô hàng loại nào đều hơn?
(1 điểm) Kiểm tra khối lượng một số quả cam Vinh của hai lô hàng loại 1 và loại 2 được kết quả như sau (đơn vị: gam)
|
Loại 1 |
250 |
230 |
260 |
265 |
250 |
250 |
245 |
260 |
280 |
260 |
|
Lọai 2 |
200 |
180 |
210 |
220 |
185 |
210 |
215 |
190 |
195 |
190 |
a) Hãy tìm khoảng biến thiên, khoảng tứ phân vị, độ lệch chuẩn của khối lượng cam Vinh ở mỗi loại.
b) Khối lượng cam Vinh ở lô hàng loại nào đều hơn?
Câu hỏi trong đề: Bộ 10 đề thi cuối kì 1 Toán 10 Kết nối tri thức có đáp án !!
Quảng cáo
Trả lời:
Sắp xếp khối lượng các quả cam Vinh ở hai lô hàng loại 1 và loại 2 theo thứ tự không giảm ta được:
|
Loại 1 |
230 |
245 |
250 |
250 |
250 |
260 |
260 |
260 |
265 |
280 |
|
Lọai 2 |
180 |
185 |
190 |
190 |
195 |
200 |
210 |
210 |
215 |
220 |
a) * Đối với lô hàng loại 1:
Khối lượng cao nhất và khối lượng thấp nhất tương ứng là 280 và 230. Do đó, khoảng biến thiên của lô hàng loại 1 là \({R_1} = 280 - 230 = 50\).
Mẫu có 10 số liệu nên trung vị hay tứ phân vị thứ hai của lô hàng loại 1 là trung bình cộng của số thứ 5 và 6. Do đó, \({Q_{2\left( 1 \right)}} = \frac{{250 + 260}}{2} = 255\).
Tứ phân vị thứ nhất là trung vị của mẫu: 230 245 250 250 250. Do đó, \({Q_{1\left( 1 \right)}} = 250\).
Tứ phân vị thứ ba là trung vị của mẫu: 260 260 260 265 280. Do đó, \({Q_{3\left( 1 \right)}} = 260\).
Khi đó, khoảng tứ phân vị của lô hàng loại 1 là \[{\Delta _{Q\left( 1 \right)}} = {Q_{3\left( 1 \right)}} - {Q_{1\left( 1 \right)}} = 260 - 250 = 10\].
Khối lượng trung bình của cân nặng cam Vinh ở lô hàng loại 1 là
\(\overline {{X_1}} = \frac{{230 + 245 + 250 \cdot 3 + 260 \cdot 3 + 265 + 280}}{{10}} = 255\).
Phương sai của cân nặng cam Vinh ở lô hàng loại 1 là
\(S_1^2 = \frac{{{{\left( {230 - 255} \right)}^2} + {{\left( {245 - 255} \right)}^2} + 3 \cdot {{\left( {250 - 255} \right)}^2} + 3 \cdot {{\left( {260 - 255} \right)}^2} + {{\left( {265 - 255} \right)}^2} + {{\left( {280 - 255} \right)}^2}}}{{10}}\)
\( = 160\)
Độ lệch chuẩn của cân nặng cam Vinh ở lô hàng loại 1 là \({S_1} = \sqrt {S_1^2} = \sqrt {160} \approx 12,65\).
* Đối với lô hàng loại 2:
Khối lượng cao nhất và khối lượng thấp nhất tương ứng là 220 và 180. Do đó, khoảng biến thiên của lô hàng loại 2 là \({R_2} = 220 - 180 = 40\).
Mẫu có 10 số liệu nên trung vị hay tứ phân vị thứ hai của lô hàng loại 2 là trung bình cộng của số thứ 5 và 6. Do đó, \({Q_{2\left( 2 \right)}} = \frac{{195 + 200}}{2} = 197,5\).
Tứ phân vị thứ nhất là trung vị của mẫu: 180 185 190 190 195. Do đó, \({Q_{1\left( 2 \right)}} = 190\).
Tứ phân vị thứ ba là trung vị của mẫu: 200 210 210 215 220. Do đó, \({Q_{3\left( 2 \right)}} = 210\).
Khi đó, khoảng tứ phân vị của lô hàng loại 2 là \[{\Delta _{Q\left( 2 \right)}} = {Q_{3\left( 2 \right)}} - {Q_{1\left( 2 \right)}} = 210 - 190 = 20\].
Khối lượng trung bình của cân nặng cam Vinh ở lô hàng loại 2 là
\(\overline {{X_2}} = \frac{{180 + 185 + 190 \cdot 2 + 195 + 200 + 210 \cdot 2 + 215 + 220}}{{10}} = 199,5\).
Phương sai của cân nặng cam Vinh ở lô hàng loại 2 là
\(S_2^2 = \frac{{{{\left( {1800 - 199,5} \right)}^2} + {{\left( {185 - 199,5} \right)}^2} + 2 \cdot {{\left( {190 - 199,5} \right)}^2} + ... + {{\left( {220 - 199,5} \right)}^2}}}{{10}}\)\( = 167,25\)
Độ lệch chuẩn của cân nặng cam Vinh ở lô hàng loại 2 là \({S_2} = \sqrt {S_2^2} = \sqrt {167,25} \approx 12,93\).
b) Từ các kết quả tính được ở câu a, ta nhận thấy mặc dù khoảng biến thiên của khối lượng cam Vinh ở lô hoàng loại 2 nhỏ hơn loại 1 nhưng khoảng tứ phân vị và độ lệch chuẩn của khối lượng cam Vinh ở lô hàng loại 2 lớn hơn loại 1. Mà khoảng biến thiên thường bị ảnh hưởng bởi giá trị bất thường nên ta sử dụng khoảng tứ phân vị và độ lệch chuẩn để so sánh. Như vậy ta thấy khối lượng cam Vinh ở lô hàng loại 1 đều hơn.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Sách - Sổ tay kiến thức trọng tâm Vật lí 10 VietJack - Sách 2025 theo chương trình mới cho 2k9 ( 31.000₫ )
- Trọng tâm Lí, Hóa, Sinh 10 cho cả 3 bộ KNTT, CTST và CD VietJack - Sách 2025 ( 40.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
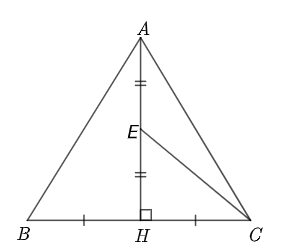
Ta có: \[\left| {\overrightarrow {CA} + \overrightarrow {CH} } \right| = \left| {2\overrightarrow {CE} } \right| = 2CE\] (với \[E\] là trung điểm của \[AH\]).
Ta lại có: \[AH = \frac{{5\sqrt 3 }}{2}\] (\[\Delta ABC\] đều, \[AH\] là đường cao), suy ra \(HE = \frac{1}{2}AH = \frac{{5\sqrt 3 }}{4}\).
\(CH = \frac{1}{2}BC = \frac{5}{2}\).
Trong tam giác \[HEC\] vuông tại \[H\], từ định lí Pythagore suy ra
\[EC = \sqrt {C{H^2} + H{E^2}} = \sqrt {{{\left( {\frac{5}{2}} \right)}^2} + {{\left( {\frac{{5\sqrt 3 }}{4}} \right)}^2}} = \frac{{5\sqrt 7 }}{4}\]
\[ \Rightarrow \left| {\overrightarrow {CA} - \overrightarrow {HC} } \right| = 2CE = \frac{{5\sqrt 7 }}{2}\].
Câu 2
Số nhân khẩu trong các hộ gia đình ở một xóm được thống kê ở bảng sau:
|
Số nhân khẩu |
1 |
2 |
3 |
4 |
5 |
|
Số hộ gia đình |
1 |
5 |
6 |
9 |
7 |
Mốt của mẫu số liệu trên là
Lời giải
Đáp án đúng là: D
Từ bảng số liệu ta thấy giá trị 4 có tần số lớn nhất (9) nên mốt của mẫu số liệu là 4.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.