Cho lục giác đều \[ABCDEF\] tâm \[O\].
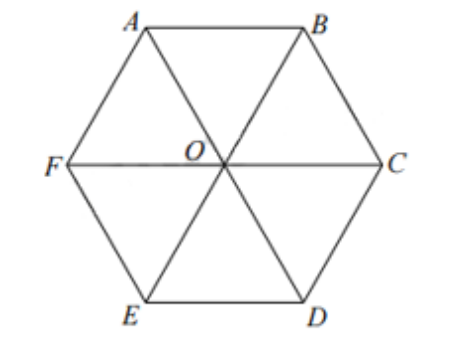
Có bao nhiêu vectơ khác không, cùng phương với vectơ \(\overrightarrow {OB} \) có điểm đầu và điểm cuối là các điểm có trên hình vẽ?
Quảng cáo
Trả lời:
Hướng dẫn giải
Đáp án đúng là: B
Các vectơ cùng phương với vecto \(\overrightarrow {OB} \) mà có điểm đầu và điểm cuối là các điểm có trên hình vẽ là các vectơ: \(\overrightarrow {BE} \), \(\overrightarrow {EB} \), \(\overrightarrow {CD} \), \(\overrightarrow {DC} \), \[\overrightarrow {AF} \], \(\overrightarrow {FA} \), \(\overrightarrow {OE} \), \(\overrightarrow {EO} \), \(\overrightarrow {BO} \).
Vậy có \[9\] vectơ thỏa mãn điều kiện.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Toán, Văn, Anh 10 cho cả 3 bộ KNTT, CTST, CD VietJack - Sách 2025 ( 13.600₫ )
- Trọng tâm Lí, Hóa, Sinh 10 cho cả 3 bộ KNTT, CTST và CD VietJack - Sách 2025 ( 40.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
Hướng dẫn giải
Đáp án đúng là: A
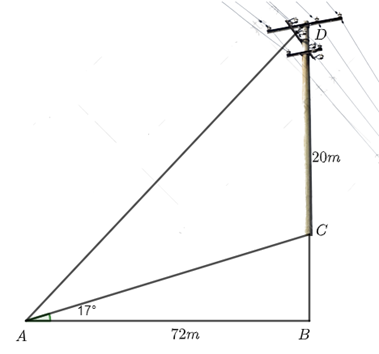
Chiều dài của dây cáp là đoạn \[AD\].
Theo bài ra ta có: \[CD = 20\,m\], \[AB = 72\,\,m\], \(\widehat {CAB} = 17^\circ \), \(\widehat {ABD} = 90^\circ \).
\[\widehat {ACB} = 180^\circ - \widehat {ACB} - \widehat {ACD} = {\rm{ }}180^\circ - 17^\circ - 90^\circ {\rm{ }} = 73^\circ \](tổng ba góc một tam giác bằng 180°).
Tam giác \[ABC\] vuông tại \[B\] , có :
\(AC = \frac{{AB}}{{\cos \widehat {CAB}}} = \frac{{72}}{{\cos 17^\circ }} \approx 75,3\,\,m\)
Áp dụng định lí cosin trong tam giác \[ACD\], ta có:
\[AD = 83,4\,\,m\]
Vậy chiều dài của dây cáp là \[83,4\,\,m\].
Câu 2
Lời giải
Hướng dẫn giải
Đáp án đúng là: A
Xét tam giác \[ABC\] có:
\(\overrightarrow {AG} = \frac{2}{3}\overrightarrow {AM} \Leftrightarrow 3\overrightarrow {AG} - 2\overrightarrow {AM} = \overrightarrow 0 \). Do đó C sai.
\(\overrightarrow {AG} = 2\overrightarrow {GM} \Leftrightarrow \overrightarrow {GA} + 2\overrightarrow {GM} = \overrightarrow 0 \). Do đó A đúng và B sai.
\(\overrightarrow {GM} = \frac{1}{3}\overrightarrow {AM} \Leftrightarrow 3\overrightarrow {GM} - \overrightarrow {AM} = \overrightarrow 0 \). Do đó D sai.
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.