(1,0 điểm). Điểm kiểm tra môn Toán của hai bạn Trung và Long trong \[6\] lần thi thử THPT Quốc gia được thống kê trong bảng dưới đây:
Lần
Tên
1
2
3
4
5
6
Trung
5
8
7
6
9
8
Long
8
4
6
8
9
6
Sử dụng kiến thức về phương sai và độ lệch chuẩn, xác định xem điểm bạn nào ổn định hơn? (làm tròn đến chữ số thập phân thứ \[2\]).
(1,0 điểm). Điểm kiểm tra môn Toán của hai bạn Trung và Long trong \[6\] lần thi thử THPT Quốc gia được thống kê trong bảng dưới đây:
|
Lần
Tên |
1 |
2 |
3 |
4 |
5 |
6 |
|
Trung |
5 |
8 |
7 |
6 |
9 |
8 |
|
Long |
8 |
4 |
6 |
8 |
9 |
6 |
Sử dụng kiến thức về phương sai và độ lệch chuẩn, xác định xem điểm bạn nào ổn định hơn? (làm tròn đến chữ số thập phân thứ \[2\]).
Quảng cáo
Trả lời:
Hướng dẫn giải:
- Điểm trung bình qua 6 lần thi thử của Trung là:
\(\overline x = \frac{{5 + 8 + 7 + 6 + 9 + 8}}{6} \approx 7,17\)
Công thức tính phương sai của một mẫu số liệu là:
\({S^2} = \frac{1}{n}\left[ {{{\left( {{x_1} - \overline x } \right)}^2} + {{\left( {{x_2} - \overline x } \right)}^2} + ... + {{\left( {{x_n} - \overline x } \right)}^2}} \right]\)
Thay số ta có:
\[{S^2} = \frac{1}{6}[{(5--7,17)^2} + {(8--7,17)^2} + {(7--7,17)^2} + {(6--7,17)^2} + {(9--7,17)^2} + {(8--7,17)^2}] \approx 1,81\]
Do đó phương sai của mẫu số liệu trên là \[1,81\].
Độ lệch chuẩn của mẫu số liệu trên là \(S = \sqrt {{S^2}} = \sqrt {1,81} \approx 1,35\).
- Điểm trung bình qua \[6\] lần thi thử của Long là:
\(\overline x = \frac{{8 + 4 + 6 + 8 + 9 + 6}}{6} \approx 6,83\)
Công thức tính phương sai của một mẫu số liệu là:
\({S^2} = \frac{1}{n}\left[ {{{\left( {{x_1} - \overline x } \right)}^2} + {{\left( {{x_2} - \overline x } \right)}^2} + ... + {{\left( {{x_n} - \overline x } \right)}^2}} \right]\)
Thay số ta có:
\[{S^2} = \frac{1}{6}[{(8--6,83)^2} + {(4--6,83)^2} + {(6--6,83)^2} + {(8--6,83)^2} + {(9--6,83)^2} + {(6--6,83)^2}] \approx 2,81\]
Do đó phương sai của mẫu số liệu trên là \[2,81\].
Độ lệch chuẩn của mẫu số liệu trên là \(S = \sqrt {{S^2}} = \sqrt {2,81} \approx 1,68\).
Ta thấy phương sai và độ lệch chuẩn trong điểm của Trung bé hơn điểm của Long nên điểm của Trung ổn định hơn.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Toán, Văn, Anh 10 cho cả 3 bộ KNTT, CTST, CD VietJack - Sách 2025 ( 13.600₫ )
- Sách - Sổ tay kiến thức trọng tâm Vật lí 10 VietJack - Sách 2025 theo chương trình mới cho 2k9 ( 31.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
Hướng dẫn giải
Đáp án đúng là: A
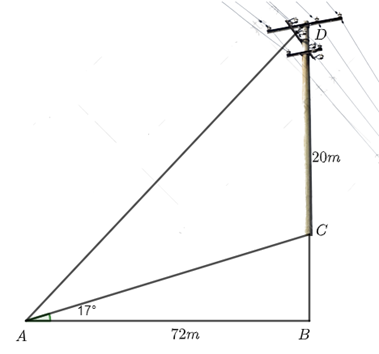
Chiều dài của dây cáp là đoạn \[AD\].
Theo bài ra ta có: \[CD = 20\,m\], \[AB = 72\,\,m\], \(\widehat {CAB} = 17^\circ \), \(\widehat {ABD} = 90^\circ \).
\[\widehat {ACB} = 180^\circ - \widehat {ACB} - \widehat {ACD} = {\rm{ }}180^\circ - 17^\circ - 90^\circ {\rm{ }} = 73^\circ \](tổng ba góc một tam giác bằng 180°).
Tam giác \[ABC\] vuông tại \[B\] , có :
\(AC = \frac{{AB}}{{\cos \widehat {CAB}}} = \frac{{72}}{{\cos 17^\circ }} \approx 75,3\,\,m\)
Áp dụng định lí cosin trong tam giác \[ACD\], ta có:
\[AD = 83,4\,\,m\]
Vậy chiều dài của dây cáp là \[83,4\,\,m\].
Câu 2
Lời giải
Hướng dẫn giải
Đáp án đúng là B
Ta có độ dài gần đúng của cây thước là \(a = 45\) với độ chính xác \(d = 0,2\) nên sai số tuyệt đối \({\Delta _{45}} \le 0,2\)
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.